Control Difuso¶
Es un sistema de control que esta basado en la lógica difusa.

Lofti A. Zadeh desarrollo la lógica difusa. Aunque la lógica difusa se había estado estudiando desde aproximadamente Los años 1920, Lofti Zadeh fue quien oficialmente introdujo el tema en 1965. El observó que los computadores no les iba bien manejando datos subjetivos Tales que si podían ser manejados por humanos.
Ejemplo calor¶
¿Está el té caliente?
- En sistemas booleanos, tenemos valores absolutos:
- En sistemas difusos, tenemos valores que son parcialmente verdaderos y parcialmente falsos
Ejemplo Humedad¶
¿Qué tan mojada esta la ropa?
En sistemas booleanos, tenemos valores absolutos:
- Mojada (Verdadero)
- Seca (Falso)
En sistemas difusos, tenemos valores que son parcialmente verdaderos y parcialmente falsos
- Parcialmente Mojada (0.7)
- Parcialmente Seca (0.3)
Lógica difusa¶
¿Que tan mojada esta la ropa?
- Lógica clásica: Verdadero (mojado), Falso (seco)
Lógica difusa: Parcialmente verdarero, parcialmente falso.
$$M \in [0,1]$$
Muy seca, poco seca, poco mojada, muy mojada
from IPython import display
myScript = """
<div>...</div>
<style type="text/css">
.input-hidden {
display: none;
}
</style>
<script>
inputToggle = function(id){
input = document.getElementById(id).getElementsByClassName("jp-Cell-inputWrapper")[0];
if(input.getAttribute("hidden")==="1"){
input.setAttribute("hidden",0);
input.classList.remove("input-hidden")
}else{
input.setAttribute("hidden",1);
input.classList.add("input-hidden")
}
}
setToggle= function(){
console.log("hidding");
codeCells = document.getElementsByClassName("jp-CodeCell");
for(var c =0; c<codeCells.length; c++){
let cc = codeCells[c]
cc.onclick = function(){
inputToggle(cc.id);
};
inputToggle(cc.id);
}
}
setTimeout(setToggle, 5000);
</script>
"""
display.display_html(myScript, raw=True)
Ventajas del control difuso¶
No requiere conocer el modelo dinámico del sistema a controlar. Por tanto,
- El control difuso no requiere identificar el sistema
- Ni necesita aproximar el modelo
- Ni necesita linealizarlo
Facilita el diseño del controlador
Pero necesita conocer las reglas lingüísticas de control de un experto. Cuando no se conoce el modelo se usa:
- Control PID (una entrada y una salida)
- Control Difuso (múltiples entradas y salidas)
Aplicaciones del control difuso¶
- ¿En qué aplicaciones se puede usar el control difuso?
Etapas dentro de un controlador difuso¶
- Valores de Entrada (crisp inputs)
- Módulo de Fusificación
- Entradas difusas
- Módulo de Inferencia
- Conclusiones difusas
- Módulo de Defusificación
- Valores de Salida (crisp outputs)
Reglas de Control¶
Dado un sistema con dos entradas $X$ y $Y$ y una salida $Z$, podemos definir las reglas de control en el modulo de inferencia así:
- Si $X$ es $A_1$ y $Y$ es $B_1$, entonces $Z$ es $C_1$
- Si $X$ es $A_2$ y $Y$ es $B_2$, entonces $Z$ es $C_2$
- Si $X$ es $A_3$ y $Y$ es $B_3$, entonces $Z$ es $C_3$
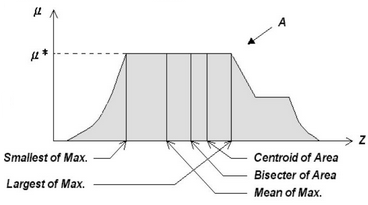
Modulo de Defusificación¶
Para la defusificación se pueden usar diferentes métodos:
- Centroide: considera a la función como una función de distribución de masa y busca su centroide.
- Bisectriz: divide el area bajo la función en dos regiones iguales.
- Máximo central (MOM mean of maximum): toma el promedio de los máximos.
- Máximo más grande (LOM largest of maximum): toma el máximo más grande.
- Máximo más pequeño (SOM smallest of maximum): toma el máximo más pequeño.
Modulo de inferencia¶
Existen diferentes métodos de inferencia, entre ellos:
- Mamdani
- Sugeno
Más información sobre estos sistemas de inferencia.
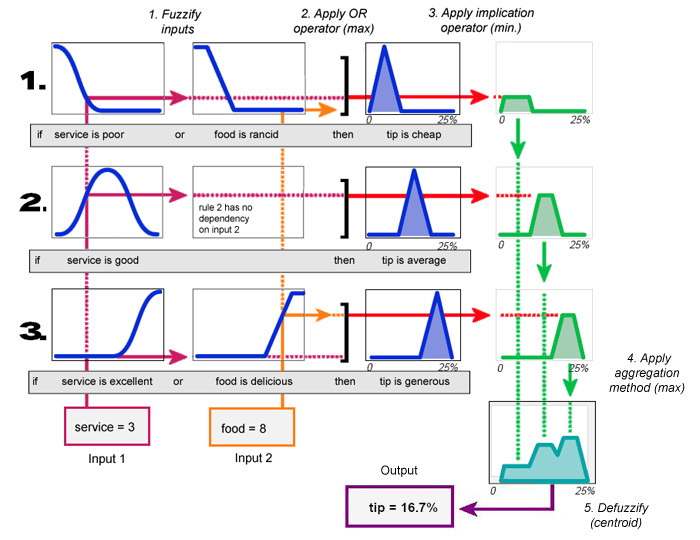
Ejemplo de la propina con Mamdani¶
Funciones de membresia¶
Empecemos con el servicio
service = ctrl.Antecedent(np.arange(0, 11, 1), 'service')
service.automf(3,names=['poor','good','excellent'])
service.view()
Funciones de membresia para la comida
food = ctrl.Antecedent(np.arange(0, 11, 1), 'food')
food['rancid'] = fuzz.trapmf(food.universe, [0,0,1,3])
food['delicious'] = fuzz.trapmf(food.universe, [7,9,10,10])
food.view()
Funciones de membresia para la propina
tip = ctrl.Consequent(np.arange(0, 25.1, 0.5), 'tip')
tip['cheap'] = fuzz.trimf(tip.universe, [0, 5, 10])
tip['average'] = fuzz.trimf(tip.universe, [8, 12.5, 18])
tip['generous'] = fuzz.trimf(tip.universe, [15, 20, 25])
tip.view()
Definimos las reglas del sistema
rule1 = ctrl.Rule(service['poor'] | food['rancid'], tip['cheap'])
rule2 = ctrl.Rule(service['good'], tip['average'])
rule3 = ctrl.Rule(service['excellent'] | food['delicious'], tip['generous'])
tipping_ctrl = ctrl.ControlSystem([rule1, rule2, rule3])
tipping = ctrl.ControlSystemSimulation(tipping_ctrl)
Con el sistema de control difuso tendremos, aquí tenemos diferencias con la imagen por que las funciones de membresia no son iguales.
tipping.input['service'] = 3
tipping.input['food'] = 8
tipping.compute()
print("Propina de %.1f%%"%tipping.output['tip'])
tip.view(sim=tipping)
Propina de 12.9%
Analisis del espacio de exploración
# We can simulate at higher resolution with full accuracy
upsampled = np.linspace(0, 10, 21)
x, y = np.meshgrid(upsampled, upsampled)
z = np.zeros_like(x)
# Loop through the system 21*21 times to collect the control surface
for i in range(21):
for j in range(21):
tipping.input['service'] = x[i, j]
tipping.input['food'] = y[i, j]
tipping.compute()
z[i, j] = tipping.output['tip']
cset = plt.contourf(x, y, z, cmap='viridis')
plt.xlabel("service");
plt.ylabel("food");
Ejemplo : Impresora¶
Realicemos el control de posición de la impresora via el voltaje del motor con un controlador difuso.
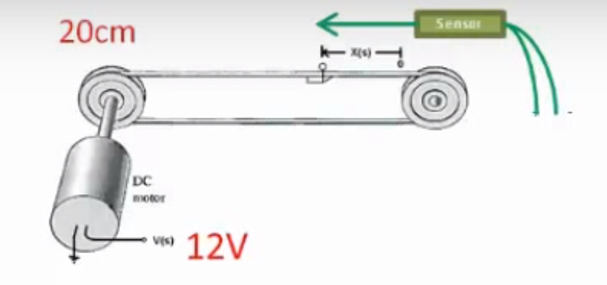
- Variable de entrada : Error de posición
- Variable de salida : Voltaje del motor
Sistema de control¶
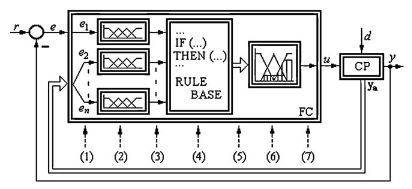
Reglas de control¶
- Si el error es NG, entonces el voltaje es NG (negativo grande)
- Si el error es NP, entonces el voltaje es NP (negativo pequeño)
- Si el error es C, entonces el voltaje es C (cero)
- Si el error es PP, entonces el voltaje es PP (positivo pequeño)
- Si el error es PG, entonces el voltaje es PG (positivo grande)
En MATLAB¶
Usaremos la aplicación fuzzy logic designer, debemos tener instalado el Fuzzy Logic Toolbox
Fuzzy logic designer¶
Esta es la ventana inicial, donde definiremos la variable de entrada como el error y la variable de salida como el voltaje.
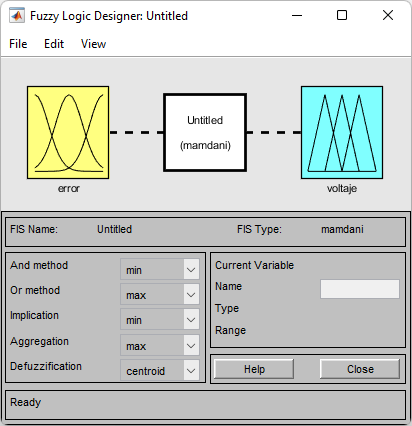
Funciones de membresia¶
Cambiar los valores de error en posición
- ENG = (Range -20, 20, Type: Trapmf, Params: -20 -20 -10 – 5)
- ENP = (Range -20, 20, Type: Trimf, Params: -10 -5 -0 )
- EC = (Range -20, 20, Type: Trimf, Params: -5 -0 5 )
- EPP = (Range -20, 20, Type: Trimf, Params: 0 5 10 )
- EPG = (Range -20, 20, Type: Trápmf, Params: 5 10 20 20 )
Funciones de membresia¶
Cambiar los valores de voltaje
- VNG = (Range -12, 12, Type: Trapmf, Params: -12 -12 -6 – 3)
- VNP = (Range -12, 12, Type: Trimf, Params: -6 -3 -0 )
- VC = (Range -12, 12, Type: Trimf, Params: -3 -0 3 )
- VPP = (Range -12, 12, Type: Trimf, Params: 0 3 6 )
- VPG = (Range -12, 12, Type: Trapmf, Params: 3 6 12 12 )
Añadir reglas de control¶
- Vamos a edit y buscamos el término Rules.
- Emparejamos las entradas y salidas correspondientes con el bóton "Add rule"
- Cuando hayamos terminado cerramos la ventana.
- Seleccionamos el metodo de fusificación.
- Exportamos las reglas.
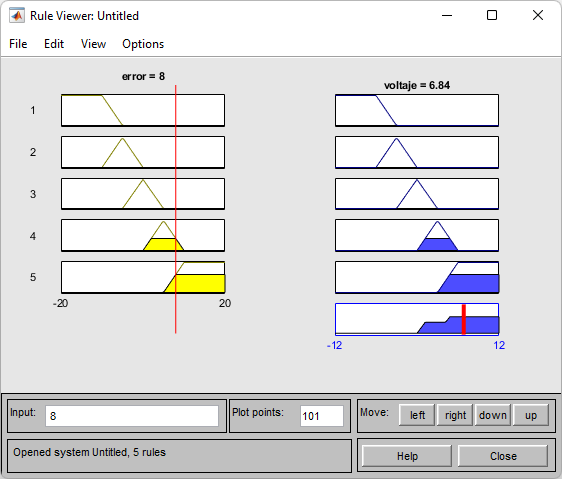
Visualización de las reglas¶
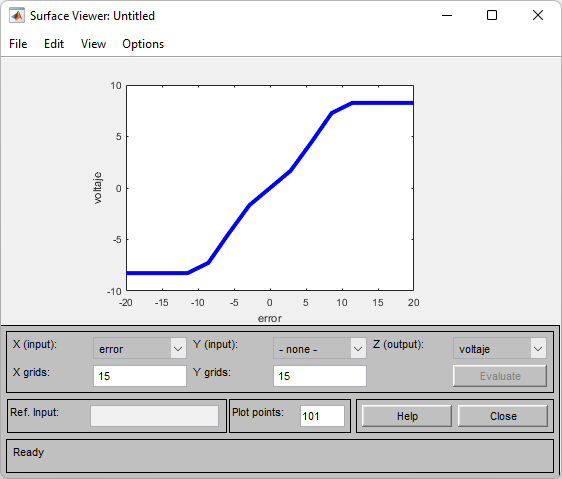
Visualización de la superficie de control¶
Archivos para Matlab¶
En Python¶
Empecemos con la función de membresía de la entrada, el error
from skfuzzy import control as ctrl
error = ctrl.Antecedent(np.arange(-20,20,1), 'error')
error['ENG'] = fuzz.trapmf(error.universe, [-20,-20,-10,-5])
error['EN'] = fuzz.trimf(error.universe, [-10,-5,0])
error['EC'] = fuzz.trimf(error.universe, [-5,0,5])
error['EP'] = fuzz.trimf(error.universe, [0,5,10])
error['EPG'] = fuzz.trapmf(error.universe, [5,10,20,20])
error.view()
Función de membresía para la salida, el voltaje
voltaje = ctrl.Consequent(np.arange(-12,12,0.1), 'voltaje')
voltaje['VNG'] = fuzz.trapmf(voltaje.universe, [-12,-12,-6,-3])
voltaje['VN'] = fuzz.trimf(voltaje.universe, [-6,-3,0])
voltaje['VC'] = fuzz.trimf(voltaje.universe, [-3,0,3])
voltaje['VP'] = fuzz.trimf(voltaje.universe, [0,3,6])
voltaje['VPG'] = fuzz.trapmf(voltaje.universe, [3,6,12,12])
voltaje.view()
Definimos las reglas del controlador:
- Si el error es NG, entonces el voltaje es NG (negativo grande)
- Si el error es NP, entonces el voltaje es NP (negativo pequeño)
- Si el error es C, entonces el voltaje es C (cero)
- Si el error es PP, entonces el voltaje es PP (positivo pequeño)
- Si el error es PG, entonces el voltaje es PG (positivo grande)
rule1 = ctrl.Rule(error['ENG'], voltaje['VNG'])
rule2 = ctrl.Rule(error['EN'], voltaje['VN'])
rule3 = ctrl.Rule(error['EC'], voltaje['VC'])
rule4 = ctrl.Rule(error['EP'], voltaje['VP'])
rule5 = ctrl.Rule(error['EPG'], voltaje['VPG'])
Creamos el controlador
controlador_ctrl = ctrl.ControlSystem([rule1, rule2, rule3, rule4, rule5])
controlador = ctrl.ControlSystemSimulation(controlador_ctrl)
controlador.input['error'] = 8
controlador.compute()
print(controlador.output['voltaje'])
voltaje.view(sim=controlador)
6.726499999999961
Visualizamos la superficie de control
errorRange = np.linspace(-20,20,15)
voltageRange = []
for e in errorRange:
controlador.input['error'] = e
controlador.compute()
voltageRange.append(controlador.output['voltaje'])
plt.plot(errorRange,voltageRange);
Demostración con el balancín¶
Construyamos un controlador difuso para el sistema mostrado a continuación:

Para esto usaremos una ecuación diferencial sencilla como modelo:
$$\ddot{x}(t) = g \sin(\alpha(t))$$try:
import control.matlab as ml
except:
!pip install control
import control.matlab as ml
Control clásico P¶
Usando un control proporcional clasico podemos ver que el sistema no se controla (sistema criticamente estable):
Kp = 1
g = 9.81; dt = 0.001; r = 0
t = [0]; e = [0]; u = [0];
xpp= [0]; xp = [0]; x = [2];
for i,ti in enumerate(np.arange(0,10,dt)):
t.append(t[-1]+dt)
e.append(r-x[-1])
u.append(min(15*np.pi/180,max(-15*np.pi/180,Kp*e[-1])))
xpp.append(g*np.sin(u[-1]))
xp.append(xp[-1] + xpp[-1]*dt)
x.append(x[-1] + xp[-1]*dt)
plt.plot(t,x);
Control clásico PD¶
Usando un control proporcional-derivativo clásico podemos ver que el sistema se comporta de la siguiente forma:
Kp = 0.5; Kd = 0.4
g = 9.81; dt = 0.001; r = 0
t = [0]; e = [0]; ea = [0]; u = [0]
xpp= [0]; xp = [0]; x = [2];
for i,ti in enumerate(np.arange(0,10,dt)):
t.append(t[-1]+dt)
e.append(r-x[-1])
de = (e[-1]-ea[-1])/dt
ea.append(e[-1])
us = Kp*e[-1] + Kd*de
u.append(min(15*np.pi/180,max(-15*np.pi/180,us)))
xpp.append(g*np.sin(u[-1]))
xp.append(xp[-1] + xpp[-1]*dt)
x.append(x[-1] + xp[-1]*dt)
plt.plot(t,x);
Controlador difuso¶
Para el controlador difuso, tenemos dos entradas el error y la derivada del error. Y una salida que es el ángulo del balancín.
from skfuzzy import control as ctrl
error = ctrl.Antecedent(np.arange(-5,5,0.05), 'error')
error.automf(5,names=['ENG','EN','EC','EP','EPG'])
error.view()
de = ctrl.Antecedent(np.arange(-1,1,0.01), 'de')
de.automf(5,names=['DENG','DEN','DEC','DEP','DEPG'])
de.view()
angle = ctrl.Consequent(np.arange(-12,12,0.1), 'angle')
angle.automf(5,names=['ANG','AN','AC','AP','APG'])
angle.view()
rule1 = ctrl.Rule(error['ENG'], angle['ANG'])
rule2 = ctrl.Rule(error['EN'], angle['AN'])
rule3 = ctrl.Rule(error['EC'], angle['AC'])
rule4 = ctrl.Rule(error['EP'], angle['AP'])
rule5 = ctrl.Rule(error['EPG'], angle['APG'])
controlador_ctrl = ctrl.ControlSystem([rule1, rule2, rule3, rule4, rule5])
controlador = ctrl.ControlSystemSimulation(controlador_ctrl)
controlador.input['error'] = 8
# controlador.input['de'] = 0
controlador.compute()
print(controlador.output['angle'])
angle.view(sim=controlador)
9.90812501458807
errorRange = np.linspace(-20,20,15)
angleRange = []
for e in errorRange:
controlador.input['error'] = e
controlador.compute()
angleRange.append(controlador.output['angle'])
plt.plot(errorRange,angleRange);
g = 9.81; dt = 0.01; r = 0
t = [0]; e = [0]; ea = [0]; u = [0]
xpp= [0]; xp = [0]; x = [2];
for i,ti in enumerate(np.arange(0,50,dt)):
t.append(t[-1]+dt)
e.append(r-x[-1])
de = (e[-1]-ea[-1])/dt
ea.append(e[-1])
controlador.input['error'] = e[-1]
controlador.compute()
us = controlador.output['angle']
u.append(us*np.pi/180)
xpp.append(g*np.sin(u[-1]))
xp.append(xp[-1] + xpp[-1]*dt)
x.append(x[-1] + xp[-1]*dt)
plt.plot(t,x,t,xp);