Introducción al Control¶
"como hacer plataformas moviles moverse efectiva, segura, predecible y colaborativamente usando teorias de control modernas"
Introducción al Control¶
Entender los conceptos asociados al control
Juego de Palabras¶
Encontremos palabras asociadas a los siguientes terminos:
- control
- producto
- mecatrónica
- sistema
- automático
- proceso
- realimentación
- lazo cerrado
- lazo abierto
- sensor
- actuador
Ejemplos de control¶
display(IFrame("https://www.youtube.com/embed/videoseries?list=PLMUWUECzl9GIKfCRF1rKLkw-deF3Y7Ppo&enablejsapi=1",width="100%",height="400px"))
Elementos básicos¶
- Estado : Representación de lo que esta haciendo el sistema actualmente.
- Dinámica : Descripción de como evolucionan los estados.
- Referencia : Que queremos que el sistema haga.
- Salida : Medidas (de algunos aspectos) del sistema.
- Entrada : Señal de control.
- Realimentación : Mapeo entre las salidas a las entradas.
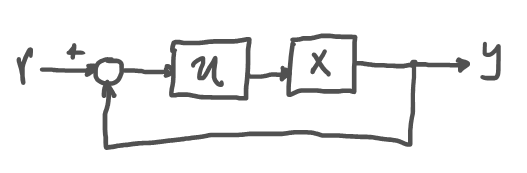
Sobre la necesidad de un modelo¶
¿Cómo seleccionamos la señal de entrada $u$?
Objetivos a la hora de seleccionar un controlador¶
- Estabilidad
- Seguimiento de la referencia
- Robustez
- Insensibilidad a las perturbaciones
- Optimalidad
Modelos dinámicos¶
Las estrategias efectivas de control se bazan en modelos predictivos.
En la actualidad debemos pasar todos los modelos a modelos discretos:
$$x_{k+1} = f\left(x_k,u_k\right)$$e.g. un reloj:
$$x_{k+1} = x_k + 1$$Reloj en tiempo discreto¶
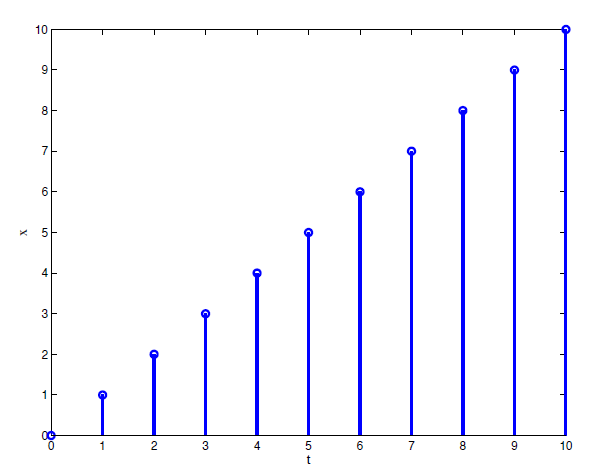
Dinámica > cambio en el tiempo¶
Las leyes de la física todas están en tiempo continuo, en vez de pensar en el siguiente estado, tenemos derivadas con respecto al tiempo
Tiempo continuo:
$$\frac{dx}{dt}=f\left(x,u\right) \qquad - \qquad \dot{x}=f\left(x,u\right)$$e.g. un reloj:
$$\dot{x} = 1$$Reloj en tiempo continuo¶
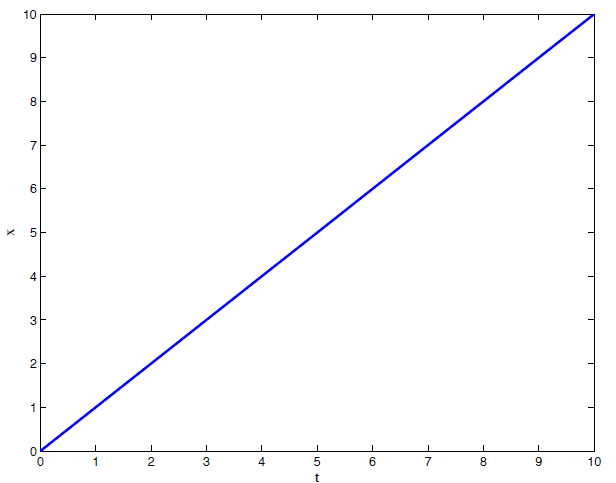
De tiempo continuo a tiempo discreto¶
En la implementación de un controlador todo esta discretizado, o muestreado:
$$\dot{x}=f\left(x,u\right)$$Con un tiempo de muestreo de $\delta t$, tenemos
$$x_k = x(k\delta t) \qquad \to \qquad x_{k+1}=x((k+1)\delta t) = ??$$$$x(k\delta t + \delta t) \approx x(k \delta t) + \delta t \, \dot{x}(k\delta t)$$$$x_{k+1} = x_k + \delta t \, f(x_k,u_k)$$Ejemplo : Controlador de velocidad crucero¶
Hagamos que un carro se mantenga a la velocidad deseada, la velocidad de referencia $r$:
Sabemos de la segunda ley de Newton:
$$F=m\,a$$- El estado del sistema es : la velocidad $x$
- La entrada del sistema es : la fuerza del motor o el freno $u$ relacionado con $F=c\,u$ con $c$ siendo un coeficiente de transmisión electro-mecánica
- La dinámica es:
Diseño de un controlador¶
- Asumamos que medimos la velocidad ($y=x$)
- La señal de control debería ser entonces función de la diferencia de $r-y$ ($=e$)
¿Cuales deben ser las propiedades de la señal de control?
- Pequeños $e$ deben dar pequeñas $u$.
- la señal $u$ no debe tener movimiento bruscos.
- la señal $u$ no debe depender de que tan bien conocemos los parámetros $c$ y $m$.
Intento de controlador¶
Modelo del carro:
$$\dot{x}=\frac{c}{m}u$$queremos que $x\to r$ cuando $t \to \infty$ o lo que es lo mismo $e \to 0$ (e=r-x)
Intento #1 de controlador
$$u = \cases{ u_{max} & si e>0\cr -u_{max} & si e<0\cr 0 & si e=0 } $$Con este controlador tendresmo un aceleraciones bruscas y dañaremos los actuadores.
Controlador tipo P¶
El problema del controlador anterior es que sobre reacciona a pequeños errores.
Intento #2 de Controlador
$$u=k\,e$$- Pequeños errores generar pequeñas señales de control.
- Señales de control suaves.
- Es conocido como un controlador proporcional.
Estabilidad pero no seguimiento del objetivo¶
Discrepancia : El modelo "real" tiene en cuenta la resistencia con el viento:
$$\dot{x} = \frac{c}{m}\,u - \gamma\,x$$Este es el modelo usado para simular el controlador. Por lo que en estado estacionario tendremos un error diferente de cero.
Calculemos el error.
Error en estado estacionario para un control P¶
Sabemos que $u=k\,e$ y tenemos que $e = r-x$ de esto, replazando en la ecuación anterior:
$$\dot{x} = \frac{c}{m}\,k(r-x) - \gamma\,x = 0$$luego,
$$ x = \frac{ck}{ck+\gamma m}r < r$$de aquí vemos que $x$ será diferente de $r$ a menos que $k \to \infty$ ($k$ tienda a infinito)
Objetivo de rendimiento¶
Un controlador debe:
- Ser estable
- Seguir el objetivo
- Ser robusto
El model:
$$\dot{x} = \frac{c}{m}\,u - \gamma\,x$$Intento #3 de Controlador
$$u = k\, e + \gamma \frac{m}{c}x$$entonces:
$$\dot{x}=0=\frac{c}{m}k(r-x)+\gamma\,x-\gamma,x \quad\to\quad x=r$$Seguimiento... pero, tenemos que conocer todos los parámetros físicos. Algo que no es posible.
Intento #4¶
Controlador PI:
$$u(t) = k_P\, e(t)+k_I\int_0^te(\tau)d\tau$$Controlador PID:
$$u(t) = k_P\, e(t)+k_I\int_0^te(\tau)d\tau + k_D \frac{de(t)}{dt}$$Control PID¶
$$u(t) = k_P\, e(t)+k_I\int_0^te(\tau)d\tau + k_D \frac{de(t)}{dt}$$- P : Contribuye a la estabilidad, y a la respuesta media
- I : Contribuye al seguimiento del objetivo y al rechazo de las perturbaciones. También contribure a la respuesta lenta. Puede causar oscilaciones.
- D : Contribuye a la respuesta rápida. Es sensible al ruido.
El PID es el controlador de bajo nivel más utilizado, la estabilidad no esta garantizada.
La realimentación tiene una gran habilidad para ser robusta al desconocimiento de los parámetros
Controlador de velocidad cruzero¶
- Modelo
- Parámetros
Implementación de una derivada¶
Cómo podemos implementar la derivada de manera discreta (tiempo de muestreo $\Delta t$):
$$\dot{e}=\frac{e_{nuevo}-e_{viejo}}{\Delta t}$$Implementación de una integral¶
Cómo podemos implementar la integral de manera discreta (tiempo de muestreo $\Delta t$):
$$\int_0^t e(\tau) d\tau \approx \sum_{k=0}^N e(k\Delta t)\Delta t = \Delta t E$$luego,
$$\Delta t E_{new} = \Delta t \sum_{k=0}^{N+1} e(k\Delta t) = \Delta t e((N+1)\Delta t) + \Delta t E_{old}$$en otras palabras,
$$E_{new}=E_{old} + e$$Implementación¶
Cada vez que el controlador es llamado:
read e;
e_dot = e - old_e;
E = E + e;
u = kP*e + kD*e_dot + kI*E;
old_e = e;
Nota: Los coeficientes del controlador deben incluir el tiempo de muestreo.