Modelizado Experimental¶
Vamos a encontrar el modelo matemático del siguiente sistema usando datos experimentales.

La planta es un sistema de iluminación con un LED de potencia (actuador) y un LDR (sensor). Este sistema es controlado a través de un Arduino Mega (actualmente Arduino Mega, en la foto Arduino Uno).
Un versión para MATLAB puede ser consultada aquí
Toma de datos¶
Para la toma de datos usaremos el código en lazo_abierto para Arduino. Y seguiremos los pasos mostrado a continuación.
- Descargamos el código.
- Subimos el código al Arduino.
- Abrimos el monitor serial.
- Copiamos los datos de un ciclo completo de apagado y prendido.
- Pegamos en un archivo llamado
datos.csvcon nombre de las columnast,u,y. - Finalmente, importamos los datos en el Colaboratory o Jupyter Notebook con pandas.
datos = pd.read_csv("datos.csv")
A continuación se muestran algunos datos.
datos
| t | u | y | |
|---|---|---|---|
| 0 | 60968004 | 0 | 455 |
| 1 | 60972004 | 0 | 454 |
| 2 | 60976004 | 0 | 455 |
| 3 | 60980004 | 0 | 455 |
| 4 | 60984004 | 0 | 455 |
| ... | ... | ... | ... |
| 253 | 61980004 | 255 | 653 |
| 254 | 61984004 | 255 | 653 |
| 255 | 61988004 | 255 | 653 |
| 256 | 61992004 | 255 | 653 |
| 257 | 61996004 | 255 | 653 |
258 rows × 3 columns
Modelizado experimental¶
Despues de importar los datos, los extraemos en vectores y graficamos.
traw = np.array(datos["t"].tolist())
uraw = np.array(datos["u"].tolist())
yraw = np.array(datos["y"].tolist())
plt.plot(traw,uraw,traw,yraw);
Para la construcción del modelo necesitamos tratar los datos, cambiaremos las unidades del tiempo que esta en microsegundos.
t = (traw - traw[0])/1e6
u = (uraw - uraw[0])
y = (yraw - yraw[0])
plt.plot(t,u,t,y);
plt.xlim((0,0.2));
Por la respuesta del sistema podemos suponer que es un sistema de primer orden con retardo. La función de transferencia para dicho sistema está dada por la expresión:
$$G(s) = \frac{\gamma}{\tau\,s+1}e^{-\theta\,s}$$Podemos suponer los valores de los parámetros y modificarlos hasta que las gráficas se parezcan.
s = tf("s")
gamma = y[-1]/u[-1]
tau = 0.0044376
theta = 0.004
num,den = pade(theta,n=5)
retardo = tf(num,den)
G = gamma/(tau*s+1)
print("------------------------")
print("Función de transferencia\n")
display(G)
GR = G*retardo
------------------------ Función de transferencia
La anterior expresión toma valores encontrados al tanteo.
T = np.linspace(t[0],t[-1],num=len(t))
ysim,tsim,_ = lsim(GR,U=u,T=T)
plt.plot(t,y,tsim,ysim,t,u);
plt.xlim((0,0.2));
Se ve que siguen habiendo diferencias entre el modelo y los datos. Aquí, podemos contruir un algoritmo de optimización que minimize el error cuadratico entre las dos respuestas (modelo y datos).
Estos son los resultados:
def model(x):
gamma, tau, theta = x
theta = max(abs(theta),0.001)
G = gamma/(tau*s+1)
num,den = pade(theta,n=5)
retardo = tf(num,den)
GR = G*retardo
ysim,tsim,_ = lsim(GR,U=u,T=T)
return np.sum((y-ysim)**2)
result = op.minimize(model,[0.77,0.005,0.004])
result
fun: 171.07466223467733
hess_inv: array([[ 3.05984796e-08, 1.03288890e-09, -3.17140679e-10],
[ 1.03288889e-09, 3.30702396e-09, -2.06624838e-09],
[-3.17140679e-10, -2.06624838e-09, 1.95079611e-09]])
jac: array([-0.18247032, 0.91336441, 2.62592506])
message: 'Desired error not necessarily achieved due to precision loss.'
nfev: 127
nit: 8
njev: 27
status: 2
success: False
x: array([0.77663225, 0.00502317, 0.00301336])
En el anterior resultado encontramos los valores optimizados para los parametros del modelo $\gamma$, $\tau$ y $\theta$. Con estos parámetros podemos verificar la respuesta nuevamente.
gamma, tau, theta = result.x
num,den = pade(theta,n=5)
retardo = tf(num,den)
G = gamma/(tau*s+1)
GR = G*retardo
print("Retardo:",theta)
Retardo: 0.0030133589411103744
T = np.linspace(t[0],t[-1],num=len(t))
ysim,tsim,_ = lsim(GR,U=u,T=T)
plt.plot(t,y,tsim,ysim,t,u);
plt.xlim((0,0.2));
Diseño de un controlador (PID)¶
Para el diseño del controlador podemos usar un controlador PID o diseñar un controlador usando la representación en espacio de estados. Primero usaremos un PID, en este caso usamos un controlador PI, y los parámetros fueron ajustados manualmente.
Kp = 2.5
Ki = 10
Kd = 0.00
K = Kp + Ki/s + Kd*s
print("Controlador PI :")
display(K)
CPID = feedback(K*GR,1)
yy,tt = step(CPID)
plt.plot(tt,yy);
Controlador PI :
'''
plt.axhline(y=0, color='k', linestyle='-')
plt.axvline(x=0, color='k', linestyle='-')
plt.plot(np.real(zero(retardo)),np.imag(zero(retardo)),"ob");
plt.plot(np.real(pole(retardo)),np.imag(pole(retardo)),"xb");
plt.plot(np.real(zero(G)),np.imag(zero(G)),"or");
plt.plot(np.real(pole(G)),np.imag(pole(G)),"xr");
plt.plot(np.real(zero(CPID)),np.imag(zero(CPID)),"og");
plt.plot(np.real(pole(CPID)),np.imag(pole(CPID)),"xg");
plt.xlim((-4000,0))
'''
print("Información de la respuesta a un escalón:\n")
stepinfo(CPID)
Información de la respuesta a un escalón:
{'RiseTime': 0.0025980221962962294,
'SettlingTime': 1.0631106827244172,
'SettlingMin': 0.4995665080555242,
'SettlingMax': 1.0219807319464205,
'Overshoot': 2.1980731946420473,
'Undershoot': 2.024617961818068,
'Peak': 1.0219807319464205,
'PeakTime': 0.007274462149629443,
'SteadyStateValue': 1.0}
Diseño de un controlador por Espacio de Estados¶
Para el diseño del controlador, debemos convertir la función de transferencia en una representación en espacio de estados:
SS = tf2ss(G)
SS
Donde la Matriz A es:
A = sp.Matrix(SS.A)
B = sp.Matrix(SS.B)
C = sp.Matrix(SS.C)
display(A)
Aquí tenemos que el valor propio de la matriz es igual al polo del sistema representado en función de transferencia.
pole(G)
array([-199.07744763+0.j])
Para el diseño de un controlador en espacio de estados podemos verificar si el sistema es completamente controlable, calculando la matriz de controlabilidad y verificando que el rango de la matriz es igual al número de variables de estado. En este caso el rango es $1$.
Gamma = ctrb(SS.A,SS.B)
display(Gamma)
matrix([[1.]])
Teniendo un sistema completamente controlable, podemos ubicar los polos del sistema en lazo cerrado donde queramos. Recordemos que para esto la realimentación se hace desde el vector de estado:
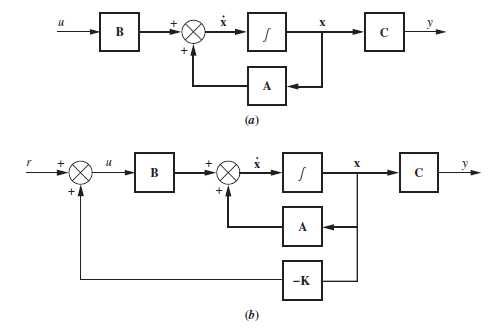
Para esto vamos a calcular la ecuación característica del sistema en lazo cerrado con variable en los elementos del controlador y vamos a igualarlas con la ecuación caracteristica resultante del posicionamiento de polos.
Para calcular la ecuación caracteristica usaremos la expresión
$$\text{det}\left(s\mathbb{I}-(A-BK)\right) = 0$$k,symS = sp.symbols("k,s")
K = sp.Matrix([[k]])
print("--------")
print("Matriz K\n")
display(K)
Ac = A-B*K
print("\n-----------")
print( "Matriz A-BK\n")
display(Ac)
det = sp.Eq((symS*sp.eye(1) - Ac).det(),0)
print("\n-----------------------")
print( "Ecuación característica\n")
display(det)
-------- Matriz K
----------- Matriz A-BK
----------------------- Ecuación característica
Si quisieramos ubicar el polo en $s=-250$ deberemos tener un polinomio tipo:
$$s+250 = 0$$luego:
comp1 = sp.Eq(sp.Poly(det.lhs,symS).coeffs()[1],250)
display(comp1)
de aquí:
sol = sp.Eq(k,sp.solve(comp1,k)[0])
display(sol)
Remplazando el valor de $k$ en la matriz dinámica en lazo cerrado tendremos:
Ac = Ac.subs({k:sol.rhs})
display(Ac)
Tendremos entonces una representación en espacio de estados para el sistema en lazo cerrado de la siguiente forma:
SS.A = np.array(Ac).astype(np.float64)
display(SS)
Con este tipo de sistema, la constante de tiempo del sistema es:
$$\tau = 1/250 = 4 \text{ milisegundos}$$Es decir un tiempo de establecimiento de $t_s = 20 \text{ ms}$
y,t = step(SS)
plt.plot(t,y);
Podemos ver que el tiempo de respuesta es correcto pero el sistema no llega al objetivo.
Para esto tenedremos que generar otro lazo cerrado e integrar la señal de error $e$.
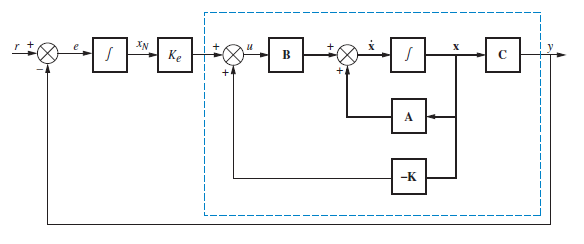
El recuadro azul tiene la siguiente representación en espacio de estados:
$$ \begin{align} \dot{x} &= (A-BK)\,x + w \\ y &= C\,x \end{align} $$del diagrama de bloques externo al recuadro tendremos las siguientes expresiones:
$$e=r-y=r-C\,x=\dot{x}_N \qquad w = K_e\,x_N$$combinando las expresiones:
$$ \begin{align} \dot{x} &= (A-BK)\,x + K_e\,x_N \\ \dot{x}_N &= -C\,x + r \\ y &= C\,x \end{align} $$Si representamos el sistema de manera matricial:
$$ \begin{align} \begin{bmatrix} \dot{x} \\ \dot{x}_N \end{bmatrix} &= \begin{bmatrix} A-BK & K_e\\ -C & 0 \end{bmatrix}& \begin{bmatrix} x \\ x_N \end{bmatrix}& + \begin{bmatrix} 0 \\ 1 \end{bmatrix}r \\ y &= \begin{bmatrix} C & 0 \end{bmatrix}& \begin{bmatrix} x \\ x_N \end{bmatrix}& \end{align} $$La nueva matriz dinámica para este sistema será:
ke = sp.symbols("K_e")
AI = sp.Matrix([[(A-B*K)[0],ke],[-C[0],0]])
display(AI)
Con la siguiente ecuación caracteristica:
det2 = sp.Eq((symS*sp.eye(2)-AI).det(),0)
display(det2)
P1 = sp.Poly(det2,symS)
Creamos una ecuación característica con los polos arbitrarios:
eq1 = sp.Eq((symS+250)*(symS+50),0)
display(eq1)
eq2 = sp.expand(eq1)
display(eq2)
P2 = sp.Poly(eq2,symS)
Igualamos los coefficientes de las dos ecuaciones características:
cP1 = P1.coeffs()
cP2 = P2.coeffs()
print("---------------------")
print("Sistema de ecuaciones\n")
for i,c in enumerate(cP1):
if i > 0:
display(sp.Eq(cP1[i],cP2[i]))
if i == 1:
eqs = {sp.Eq(cP1[i],cP2[i])}
if i > 1:
eqs.add(sp.Eq(cP1[i],cP2[i]))
print("\n---------------------------")
print( "Valores para el controlador\n")
ks = sp.solve(eqs,{k,ke})
display(ks)
--------------------- Sistema de ecuaciones
--------------------------- Valores para el controlador
Encontrando los valores del controlador, remplazamos en la matriz dinámica.
AI2 = AI.subs(ks)
AIn = np.array(AI2).astype(np.float64)
print("Matriz A\n")
display(AI2)
Matriz A
Verificamos que los valores propios si correspondan a los polos deseados:
np.linalg.eig(AIn)
(array([-250., -50.]),
array([[-0.8504964 , -0.30770401],
[-0.52598087, -0.95148213]]))
Construyamos las matrices adicionales para el sistema:
BIn = np.matrix([[0],[1]])
print("Matriz B\n")
sp.Matrix(BIn)
Matriz B
CIn = np.matrix([[SS.C[0,0],0]])
print("Matriz C\n")
sp.Matrix(CIn)
Matriz C
Luego nuestro sistema completo será
DIn = np.matrix([[0]])
SSI = ss(AIn,BIn,CIn,DIn)
display(SSI)
print("Respuesta a un escalón")
y,t = step(SSI)
plt.plot(t,y);
Respuesta a un escalón
Implementación¶
Para implementar en Arduino el controlador en espacio de estados debemos considerar:

Del diagrama de bloque tenemos que la acción $u$ es:
$$u = K_e\int_0^t e(\tau)\,d\tau - k \,x(t)$$con $e(t)=r-y(t)$ y $x(t) = C^{-1}\, y(t)$.
Esta ecuación se puede programar de la siguiente forma:
nke = ks[ke]
nkp = ks[k]/SSI.C[0,0]
print("""
float ke = %f;
float kp = %f;
float y = 0;
float u = 0;
float ref = 500;
float error = 0;
float eSum = 0;
float dt = 0.001;
void control_loop() {
error = ref - y;
eSum += error * dt;
u = ke * eSum + kp * y;
}
""" % (nke,nkp))
float ke = 80.848605;
float kp = 0.652756;
float y = 0;
float u = 0;
float ref = 500;
float error = 0;
float eSum = 0;
float dt = 0.001;
void control_loop() {
error = ref - y;
eSum += error * dt;
u = ke * eSum + kp * y;
}
código arduino lazo cerrado para el espacio de estados.
La implemntación del controlador en espacio de estado para este sistema es similar al controlador PID, luego podemos usar los mismos valores:
Kp = 0.65
Ki = 81
K = Kp + Ki/s
print("Controlador PI :")
display(K)
CPID = feedback(K*GR,1)
yy,tt = step(CPID)
plt.plot(tt,yy);
Controlador PI :