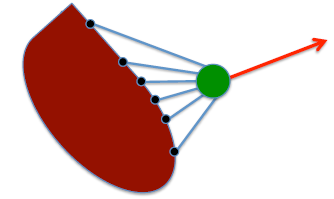
Recordando los comportamientos¶
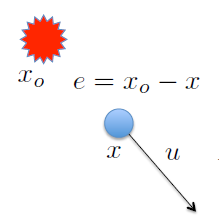
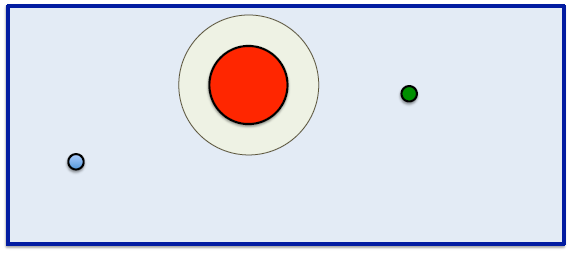
Usemos teoría de control para describir lo que ocurre en la imagen:
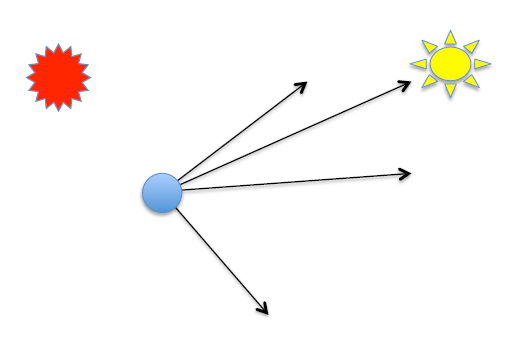
- Llegar al objetivo
- Evitar el obstaculo
Empecemos por el modelo¶
Para el proposito de planear asumamos el modelo de una particula controlada en velocidad en el plano $xy$:
$$\dot{x}=u\quad,\quad x\in\mathscr{R}^2$$cuya representación en espacio de estados es:
$$\dot{x} = \left[\array{0&0\\0&0}\right]x+\left[\array{1&0\\0&1}\right]u$$¿es este sistema controlable?
$$\Gamma = \left[\array{B&AB}\right]=\left[\array{I&0}\right]$$El duo dinámico¶
Los comportamiento principales en una plataforma movil son:
- Ir al objetivo: El robot se dirige hacia el objetivo.
- Evita obstaculos: No te golpes contra las cosas.
Tarea en el diseño del controlador:
- Seleccionar el vector de movimiento deseado y definirlo como la velocidad del vehículo.

Ir al objetivo¶
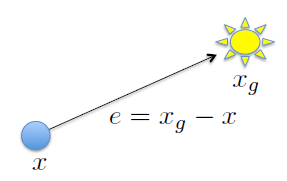
¿Es asintoticamente estable?
$$K>0 \quad\text{o}\quad K\succ0 \quad\{\text{eig}(K)>0\}$$$$e\to 0$$Una preocupación¶
- Un controlador lineal significa que el robot va más rápido entre más lejos del objetivo este.
- Una solución en la práctica: Hacemos la ganancia $K$ una función de $e$:
considerando $K$ de la siguiente forma:
$$K = v_0 \frac{1-e^{-\alpha\parallel e\parallel^2}}{\parallel e\parallel}$$alpha = 2
v0 = 1
e = np.arange(0,3,0.01)
K = v0 * (1-np.exp(-alpha*e*e))
plt.plot(e,K);
plt.ylabel("$||u||$");
plt.xlabel("$||e||$");
Para evitar obstaculos¶
Cosideremos la siguiente $K$ dependiente del error $e$:
$$K = \frac{1}{\parallel e\parallel}\left(\frac{c}{\parallel e\parallel^2 +\epsilon}\right)$$c = 0.01
epsilon = 0.01
e = np.arange(0,1,0.01)
K = c / (e*e + epsilon)
plt.plot(e,K);
plt.ylabel("$||u||$");
plt.xlabel("$||e||$");
Transiciones entre modos o comportamientos¶
- ¿Cómo acoplar la dinámica del robot con los comportamientos?
- ¿Cuáles deben ser las transiciones?
Cambios bruscos o difuminado¶
Dados dos comportamientos diferentes, como debemos combinarlos ?
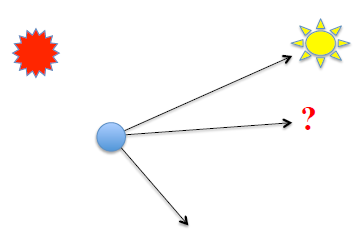
- Cambios bruscos
- Interpolación / difuminado
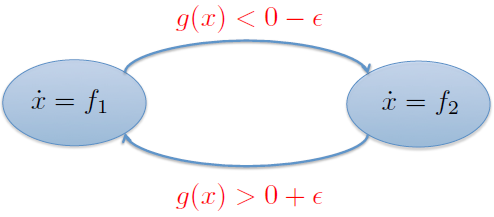
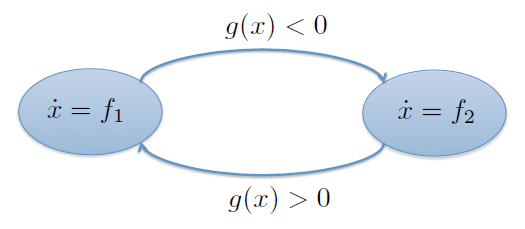
Posibilidad #1 : Autómata Híbrido¶
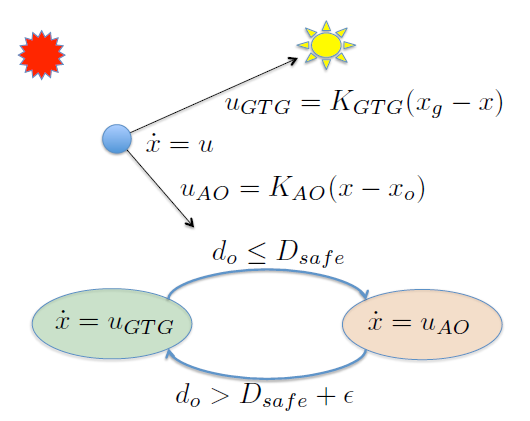
Posibilidad #2 : Modo combinado¶
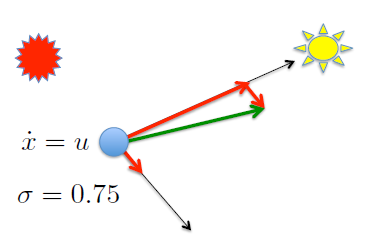
beta = 5
do = np.arange(0,1,0.01)
sigma = 1-np.exp(-beta*do)
plt.plot(do,sigma);
plt.xlabel("$d_o$");
plt.ylabel("$\sigma$");
Comentarios¶
- Dos elecciones, cada uno con ventajas y desventajas
- Que bueno sería tener las ventajas de ambas posibilidades: movimiento suave y desempeño garantizado
- Usaremos del modo inducido
Mundos convexos y no convexos¶
Veamos cuando nuestros dos comportamientos son suficientes y cuando necesitamos agregar más comportamientos.
De un mundo simple a un mundo complejo tenemos:
- El mundo de los puntos.
- El mundo de los circulos.
- El mundo de objetos convexos.
- El mundo de objetos no convexos.
- El mundo de los laberintos.
El mundo de los puntos¶
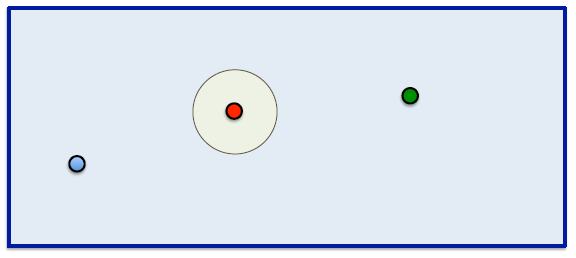
- Aquí los dos comportamientos son suficientes a menos que seamos muy de malas.
- El problema es que podemos entrar en un Zenon.
- La solución es agregar algo de ruido. En práctica siempre tendremos ruido.
Obstaculos convexos¶

Un obstaculo es convexo si cada linea trazada entre dos puntos al interior del obstaculo queda dentro del obstaculo.
El mundo de objetos convexos¶
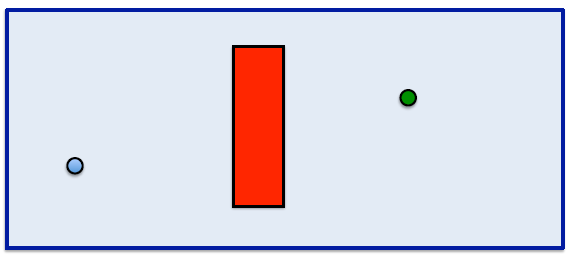
El mundo de objetos no convexos¶
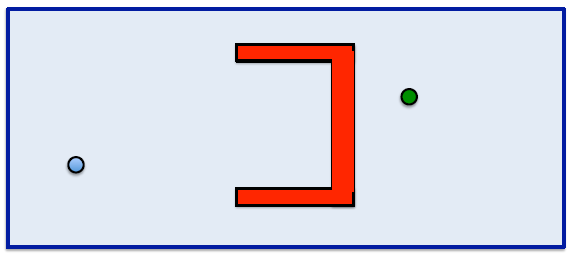
El mundo de los laberintos¶
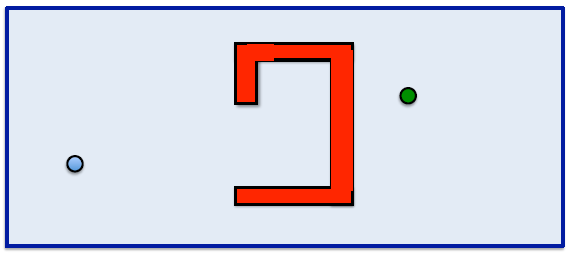
Otro comportamiento¶
Necesitamos otro comportamiento para lidiar con estos mundos que tienen obstaculos no convexos.
Seguir el muro¶
- Necesitamos una forma de lidiar con ambientes complejos.
- Un comportamiento muy útil es hacer que el robot siga la frontera de un obstaculo o muro.
- Esto también nos permite introducir el modo inducido en de forma más sistematica.
Cómo seguir un muro¶
- El comportamiento de seguir un muro debe mantener una distancia constante entre el robot y el obstaculo/muro.
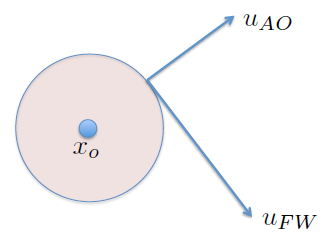
Seguimos el muro de manera¶
horaria o anti-horaria¶
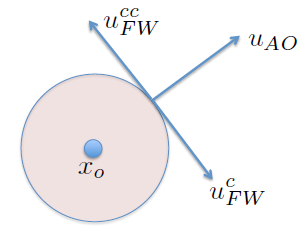
$$u_{FW}^c = \alpha R(-\pi/2) u_{AO} = \alpha \left[\array{0&1\\-1&0}\right]u_{AO}$$$$u_{FW}^{cc} = \alpha R(\pi/2) u_{AO} = \alpha \left[\array{0&-1\\1&0}\right]u_{AO}$$Matriz de rotación:
$$R(\theta) = \left[\array{\cos\theta&-\sin\theta\\\sin\theta&\cos\theta}\right]$$Horario o anti-horario ?¶

¿Qué dirección elegir?
- No hay una respuesta obvia a esto
- Tal vez podemos elegir la dirección basados en la dirección al objetivo.
Horario o anti-horario ?¶

Dificultad¶
- ¿Cuándo terminar el comportamiento seguir muro?
- ¿Existe alguna manera sistematica de escalar el comportamiento?
Modo Inducido¶
Necesitamos el comportamiento seguir-muro para resolver problemas complejos en navegación.
Vimos que podemos seguir muros usando:
$$\alpha R(\pm \pi/2) u_{AO}$$Podemos conectar todos los comportamientos que tenemos en una manera más sistematica?
La idea¶
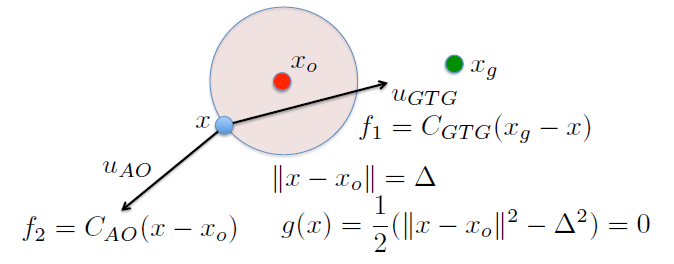
Conectandolo con el modo inducido¶
$$g(x)=\frac{1}{2}\left(\parallel x-x_o \parallel ^2 - \Delta^2\right)=0$$$$f_1 = C_{GTG}(x_g-x) \qquad\qquad f_2 = C_{AO}(x-x_o)$$El modo inducido:
$$\dot{x} = \frac{1}{L_{f_2}g - L_{f_1}g}\left(L_{f_2}g\,f_1 -L_{f_1}g\,f_2\right)$$$$\frac{\partial g}{\partial x} = (x-x_o)^T$$$$L_{f_2}g = \frac{\partial g}{\partial x} f_2 = (x-x_o)^TC_{AO}(x-x_o) = C_{AO}\parallel x-x_o \parallel^2$$$$L_{f_1}g = \frac{\partial g}{\partial x} f_1 = C_{GTG}(x-x_o)^T(x_g-x)$$Conectandolo con el modo inducido¶
El modo inducido:
$$\dot{x} = \frac{1}{L_{f_2}g - L_{f_1}g}\left(L_{f_2}g\,f_1 -L_{f_1}g\,f_2\right)$$$$\array{ L_{f_2}g =& C_{AO}\parallel x-x_o \parallel^2 \\ L_{f_1}g =& C_{GTG}(x-x_o)^T(x_g-x)}$$Recordemos:
$$\array{ u_{FW}^{c} =& \alpha R(- \pi/2) u_{AO} \\ u_{FW}^{cc} =& \alpha R(+ \pi/2) u_{AO} }$$Son lo mismo!
¿Cuando paramos el modo deslizante?¶

Podemos parar cuando hemos hecho suficiente progreso y tenemos una vista clara al objetivo.
Todo juntos¶
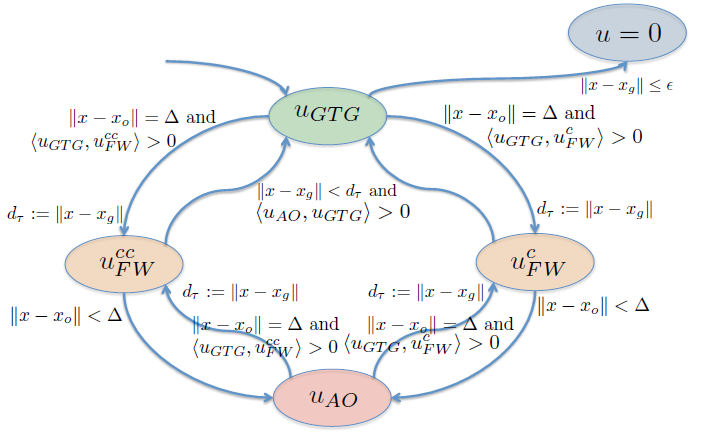
Consideraciones prácticas¶
- Obstaculos no puntuales
- Guardias con holgura
- Ajustar, ajustar, ajustar
Los obstaculos no son puntos¶
Tenemos que considerar que los obstaculos no son puntos, aunque la mayoria de sensores retornan puntos.
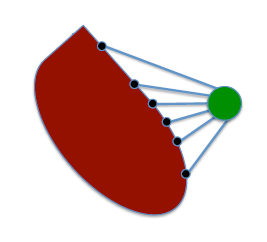
¿Cómo lidiar con ellos?
Algunas opciones¶
- Usar el punto más cercano al robot (no esta mal)
- Usar una ponderación y agregar el vector de obstaculos dependiendo de la distancia a ellos (mejor)
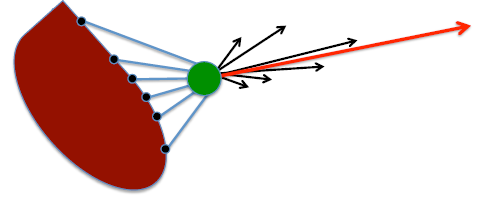
Algunas opciones¶
- Usar el punto más cercano al robot (no esta mal)
- Usar una ponderación y agregar el vector de obstaculos dependiendo de la distancia a ellos (mejor)
- Usar una ponderación dependiendo de la distancia de los obstaculos y la dirección de viaje (mucho mejor)
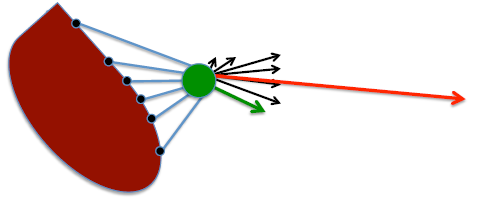
Algunas opciones¶
- Usar el punto más cercano al robot (no esta mal)
- Usar una ponderación y agregar el vector de obstaculos dependiendo de la distancia a ellos (mejor)
- Usar una ponderación dependiendo de la distancia de los obstaculos y la dirección de viaje (mucho mejor)
- Hacer un mapa y planear (ideal)

Guardias con holgura¶
Ya que los sensores no son perfectos, siempre debemos permitir una holgura en los guardias de los automatas híbridos.
Guardias con holgura¶
Ya que los sensores no son perfectos, siempre debemos permitir una holgura en los guardias de los automatas híbridos.