Plataformas móviles¶
Entendiendo la bases detrás de las plataformas
¿Cómo mover una plataforma móvil?¶
¿Qué necesitamos para llevar un robot de un punto $A$ a un punto $B$?

¿Cómo mover una plataforma móvil?¶
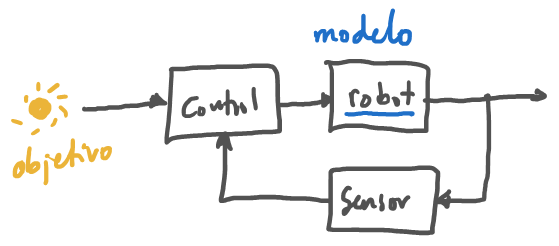
Divide y Conquista¶
- El mundo es dinámico y desconocido
- El controlador debe responder a todas las condiciones ambientales
- En vez de construir un complejo controlador, usemos la idea de divide y conquista.
División de los comportamientos¶
- Ir a la meta
- Evitar obstaculos
- Seguir el muro
- Sigue un objetivo
- ...
Comportamiento¶
display(IFrame("https://www.youtube.com/embed/Ro7T3q14uDY",width="100%",height="400px"))
Plataformas diferenciales¶
- Para controlar un sistema necesitamos su modelo.
- Las plataformas móviles diferenciales son muy comunes.
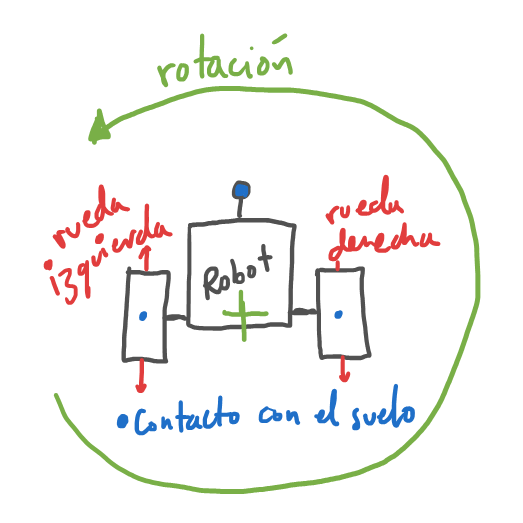
Modelo 1.0¶
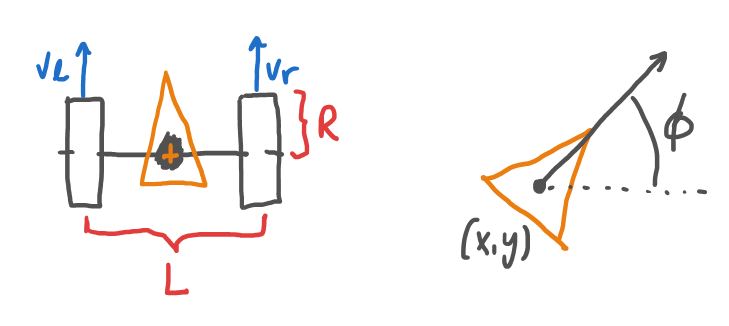
Modelo uniciclo¶
Como no es natural pensar en velocidades de las ruedas entonces vamos a ir directamente a la velocidad traslacional y rotacional.
- Entradas
- Dinámica
Modelo 2.0¶
- Se diseña para este modelo:
- Se implementa este modelo:
- en donde:
Odometria¶
- ¿Cuál es el estado del robot?
- ¿Cómo obtenemos la información del estado?
- Dos posibilidades
- Sensores externos
- Sensores internos:
- Orientación: compas,...
- Posición: acelerometro, giroscopo,
- Encoder de las ruedas
Encoder de las ruedas¶
- Los encoder dan la distancia (angular) recorrida por cada rueda
- Asumamos que las rueda describen un arco, en una pequeña escala de tiempo
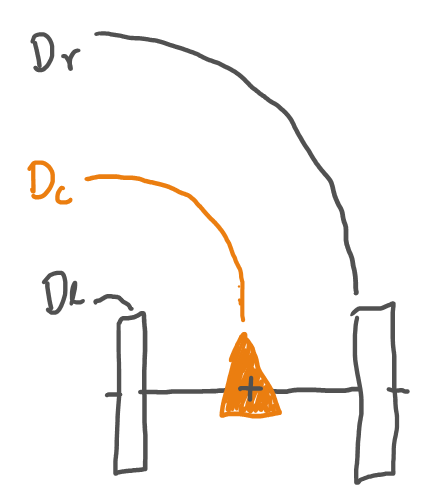 $$\cases{ x' = x + D_c \cos(\phi)\cr
y' = y + D_c \sin(\phi)\cr
\phi' = \phi + \frac{D_r-D_l}{L}
}
\qquad D_c = \frac{D_r+D_l}{2}
$$
$$\cases{ x' = x + D_c \cos(\phi)\cr
y' = y + D_c \sin(\phi)\cr
\phi' = \phi + \frac{D_r-D_l}{L}
}
\qquad D_c = \frac{D_r+D_l}{2}
$$
Encoder de las ruedas¶
- ¿Cómo sabemos cuanto se ha movido cada rueda?
- Asumimos que cada rueda tiene $N$ pulsos por revolución
- La mayoría de encoders dan un conteo de pulso desde el inicio.
- Para cada rueda:
- Calculamos la diferencia entre pulsos
- Y luego calculamos la distancia recorrida
Usar Encoders genera un gran problema
Sensores¶
Los robots necesitan saber a cerca de su mundo alrededor.
Los sesores más utilizados con una "falda" sobre el robot:
- IR
- Ultrasonido
- Lidar
Otros sensores externos incluyen
- Vision
- Tacto
- "GPS"
Abstracción de disco¶
En vez de preocuparnos por la resolución de los sensores, asumiremos que conocemos la distancia y dirección de todos los obtaculos al rededor de nosotros (que estén lo suficientemente cerca).
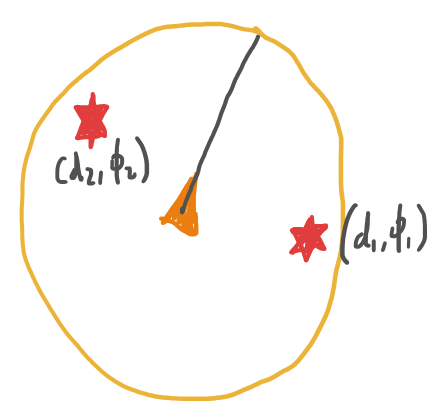
Si conocemos nuestra propia pose (posición y orientación), entonces
$$\cases{ x_1 = x + d_1 \cos(\phi_1+\phi) \\ y_1 = y + d_1 \sin(\phi_1+\phi) }$$! Ejemplo : Rendezvous¶
display(IFrame("https://cap232.davinsony.com/babylon-robot-diferencial?robots=2&password=Z29hbC5kaXNwb3NlKCk7c3lzdGVtJTVCNiU1RD0xO3N5c3RlbSU1QjEwJTVEPTE7c3lzdGVtLmxvb3A9ZnVuY3Rpb24oKSU3QngxPXN5c3RlbSU1QiUyMkEwJTIyJTVEO3kxPXN5c3RlbSU1QiUyMkExJTIyJTVEOyVDRiU5NTE9c3lzdGVtJTVCJTIyQTIlMjIlNUQ7eDI9c3lzdGVtJTVCJTIyQTMlMjIlNUQ7eTI9c3lzdGVtJTVCJTIyQTQlMjIlNUQ7JUNGJTk1Mj1zeXN0ZW0lNUIlMjJBNSUyMiU1RDslQ0YlOTVkPU1hdGguYXRhbjIoKHkyLXkxKSwoeDIteDEpKTtlMT0lQ0YlOTVkLSVDRiU5NTE7ZTE9TWF0aC5hdGFuMihNYXRoLnNpbihlMSksTWF0aC5jb3MoZTEpKTslQ0YlOTVkPU1hdGguYXRhbjIoKHkxLXkyKSwoeDEteDIpKTtlMj0lQ0YlOTVkLSVDRiU5NTI7ZTI9TWF0aC5hdGFuMihNYXRoLnNpbihlMiksTWF0aC5jb3MoZTIpKTtzeXN0ZW0lNUI3JTVEPTUqZTE7c3lzdGVtJTVCMTElNUQ9NSplMjtpZihNYXRoLmFicyh5MS15MiklM0MwLjEmJk1hdGguYWJzKHgxLXgyKSUzQzAuMSklN0JzeXN0ZW0lNUIlMjJBMCUyMiU1RD1yYW5kb21QbGFjZSgpO3N5c3RlbSU1QiUyMkExJTIyJTVEPXJhbmRvbVBsYWNlKCk7c3lzdGVtJTVCJTIyQTMlMjIlNUQ9cmFuZG9tUGxhY2UoKTtzeXN0ZW0lNUIlMjJBNCUyMiU1RD1yYW5kb21QbGFjZSgpOyU3RCU3RA==",width="100%",height="400px"))
Behavior-Based Robotics¶
Robótica basada en comportamientos

El mundo cambia constantemente y es desconocido, por lo que no tiene sentido sobre-planear. La idea clave: Desarrollar un a biblioteca de controladores utiles (comportamientos). Cambiar entre los controladores en respuesta a los cambios ambientales.
Construyendo un comportamiento (controlador)¶
Asumamos que tenemos un robot diferencial que se mueve a una velocidad translacional constante.
$$\cases{ \dot{x} = v_0 \cos(\phi)\cr \dot{y} = v_0 \sin(\phi)\cr \dot{\phi} = w } $$y queremos orientar el robot a una dirección deseada, ¿cuál debe ser el valor de $w = ?$ ?
Tenemos una referencia, un modelo, una señal de control y un seguimiento del error:
$$r=\phi_d \qquad e = \phi_d - \phi \qquad \dot{\phi}=w$$Por que no usar un PID?
$$ w = K_P \, e + K_I \int ed\tau + K_D \dot{e}$$Lidiando con el angulo¶
Normalmente esto no funciona ya que estamos lidiando con angulos y entonces:
$$\phi_d =0 \quad \phi = 100\pi \qquad \to \qquad e = -100\pi$$La solución es asegurarnos que $e \in [-\pi,\pi]$
Podemos usar el truco con atan2:
$$e' = \text{atan2}(\sin(e),\cos(e)) \in [-\pi,\pi]$$Ejemplo de Navegación¶
El problema de la navegación es ir al objetivo sin chocar con obstaculos.

Como mínimo necesitamos dos comportamientos:
- Ir al objetivo/meta
- Evitar obstaculos
Comportamiento: Ir a la meta¶
¿Cómo llevar el robot al objetivo?
$$\cases{ \dot{x} = v_0 \cos(\phi)\cr \dot{y} = v_0 \sin(\phi)\cr \dot{\phi} = w } \qquad e = \phi_d - \phi \qquad w = PID(e) $$ $$\phi_d = \arctan\left(\frac{y_m-y}{x_m-x}\right)$$
$$\phi_d = \arctan\left(\frac{y_m-y}{x_m-x}\right)$$
Primer intento¶
$$w = K (\phi_d - \phi)$$
¡Error en el cálculo de los angulos!
Primer intento simulación¶
display(IFrame("http://cap232.davinsony.com/babylon-robot-diferencial?password=cGluWG0lMjA9JTIwMjslMEFwaW5ZbSUyMD0lMjAzOyUwQXBpblYlMjAlMjA9JTIwNjslMEFwaW5XJTIwJTIwPSUyMDc7JTBBcGluWCUyMCUyMD0lMjAlMjJBMCUyMjslMEFwaW5ZJTIwJTIwPSUyMCUyMkExJTIyOyUwQXBpblBoaT0lMjAlMjJBMiUyMjslMEElMEF4bSUyMD0lMjAwOyUwQXltJTIwPSUyMDA7JTBBJTBBc3lzdGVtJTVCcGluViU1RCUyMD0lMjAxOyUwQXN5c3RlbSU1QnBpblhtJTVEJTIwPSUyMHhtOyUwQXN5c3RlbSU1QnBpblltJTVEJTIwPSUyMHltOyUwQSUwQXN5c3RlbS5sb29wJTIwPSUyMGZ1bmN0aW9uKCklN0IlMEElMEElMjAlMjB4JTIwPSUyMHN5c3RlbSU1QnBpblglNUQ7JTBBJTIwJTIweSUyMD0lMjBzeXN0ZW0lNUJwaW5ZJTVEOyUwQSUyMCUyMHBoaSUyMD0lMjBzeXN0ZW0lNUJwaW5QaGklNUQ7JTBBJTBBJTIwJTIwcGhpZCUyMD0lMjBNYXRoLmF0YW4oKHltLXkpLyh4bS14KSk7JTBBJTIwJTIwZSUyMCUyMCUyMCUyMD0lMjBwaGlkLXBoaTslMEElMEElMjAlMjBzeXN0ZW0lNUJwaW5XJTVEJTIwJTIwJTIwJTIwPSUyMGU7JTBBJTBBJTdE",width="100%",height="400px"))
Segundo intento¶
$$"w = K (\phi_d - \phi)"$$
¡Una ganancia del controlador muy bajita!
Segundo intento simulación¶
display(IFrame("http://cap232.davinsony.com/babylon-robot-diferencial?password=cGluWG0lMjA9JTIwMjslMEFwaW5ZbSUyMD0lMjAzOyUwQXBpblYlMjAlMjA9JTIwNjslMEFwaW5XJTIwJTIwPSUyMDc7JTBBcGluWCUyMCUyMD0lMjAlMjJBMCUyMjslMEFwaW5ZJTIwJTIwPSUyMCUyMkExJTIyOyUwQXBpblBoaT0lMjAlMjJBMiUyMjslMEElMEF4bSUyMD0lMjAwOyUwQXltJTIwPSUyMDA7JTBBJTBBc3lzdGVtJTVCcGluViU1RCUyMD0lMjAxOyUwQXN5c3RlbSU1QnBpblhtJTVEJTIwPSUyMHhtOyUwQXN5c3RlbSU1QnBpblltJTVEJTIwPSUyMHltOyUwQSUwQXN5c3RlbS5sb29wJTIwPSUyMGZ1bmN0aW9uKCklN0IlMEElMEElMjAlMjB4JTIwPSUyMHN5c3RlbSU1QnBpblglNUQ7JTBBJTIwJTIweSUyMD0lMjBzeXN0ZW0lNUJwaW5ZJTVEOyUwQSUyMCUyMHBoaSUyMD0lMjBzeXN0ZW0lNUJwaW5QaGklNUQ7JTBBJTBBJTIwJTIwcGhpZCUyMD0lMjBNYXRoLmF0YW4yKCh5bS15KSwoeG0teCkpOyUwQSUyMCUyMGUlMjAlMjAlMjAlMjA9JTIwcGhpZC1waGk7JTBBJTIwJTIwZSUyMCUyMCUyMCUyMD0lMjBNYXRoLmF0YW4yKE1hdGguc2luKGUpLE1hdGguY29zKGUpKTslMEElMEElMjAlMjBzeXN0ZW0lNUJwaW5XJTVEJTIwJTIwJTIwJTIwPSUyMGU7JTBBJTBBJTdE",width="100%",height="400px"))
Tercer intento¶
$$"w = K_{BIG} (\phi_d - \phi)"$$
Tercer Intento simulación¶
display(IFrame("http://cap232.davinsony.com/babylon-robot-diferencial?password=cGluWG0lMjA9JTIwMjslMEFwaW5ZbSUyMD0lMjAzOyUwQXBpblYlMjAlMjA9JTIwNjslMEFwaW5XJTIwJTIwPSUyMDc7JTBBcGluWCUyMCUyMD0lMjAlMjJBMCUyMjslMEFwaW5ZJTIwJTIwPSUyMCUyMkExJTIyOyUwQXBpblBoaT0lMjAlMjJBMiUyMjslMEElMEF4bSUyMD0lMjAwOyUwQXltJTIwPSUyMDA7JTBBJTBBc3lzdGVtJTVCcGluViU1RCUyMD0lMjAxOyUwQXN5c3RlbSU1QnBpblhtJTVEJTIwPSUyMHhtOyUwQXN5c3RlbSU1QnBpblltJTVEJTIwPSUyMHltOyUwQSUwQXN5c3RlbS5sb29wJTIwPSUyMGZ1bmN0aW9uKCklN0IlMEElMEElMjAlMjB4JTIwPSUyMHN5c3RlbSU1QnBpblglNUQ7JTBBJTIwJTIweSUyMD0lMjBzeXN0ZW0lNUJwaW5ZJTVEOyUwQSUyMCUyMHBoaSUyMD0lMjBzeXN0ZW0lNUJwaW5QaGklNUQ7JTBBJTBBJTIwJTIwcGhpZCUyMD0lMjBNYXRoLmF0YW4yKCh5bS15KSwoeG0teCkpOyUwQSUyMCUyMGUlMjAlMjAlMjAlMjA9JTIwcGhpZC1waGk7JTBBJTIwJTIwZSUyMCUyMCUyMCUyMD0lMjBNYXRoLmF0YW4yKE1hdGguc2luKGUpLE1hdGguY29zKGUpKTslMEElMEElMjAlMjBzeXN0ZW0lNUJwaW5XJTVEJTIwJTIwJTIwJTIwPSUyMDIwKmU7JTBBJTBBJTdE",width="100%",height="400px"))
¿Qué podemos hacer para que no gire locamente?
Comportamiento: Evadir obstaculos¶
¿Cómo evadir ir directamente a los obstaculos.
Podemos usar la mismaidea para definir ir a la meta?
display(IFrame("http://cap232.davinsony.com/babylon-robot-diferencial?obstacles=30",width="100%",height="400px"))
Hacia donde ir¶
$$\phi_1= \phi_{obst}+ \pi \qquad \phi_2 = \phi_{obst}\pm \pi/2 \qquad \phi_3 = \phi_{meta}$$La dirección depende de la dirección al objetivo, no puede ser puro sino combinado.
$$\phi_4 = F(\phi_{obst},\phi_{meta})$$Mecanismo de decisión¶
Este ejemplo ilustra 2 mecanismos de decisión diferentes:
- El ganador toma todo o cambios fuertes.
- Combinar comportamientos.
Las dos situaciones tienen merito en diferentes situaciones:
- Desempeño
- Análisis
Veremos con diseñar comportamientos sistematicos y mecanismos de decisión