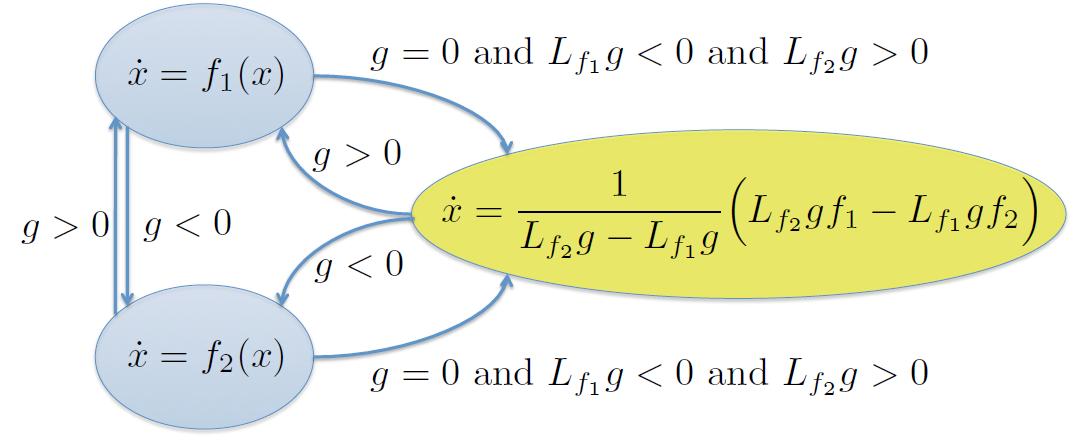Suiches en todas partes¶
Hasta el momento hemos estudiado modelos que se mantienen igual durante el tiempo. Lo que no es verdad.
Hemos diseñado controladores que sirven para todos los propositos. No es verdad en robótica.
Recordemos el enfoque de control basado en comportamiento. Necesitamos ser capaces de lidiar con todos estos tipos de fenomenos.
Los suiches aparecen como una necesidad¶
Las condiciones en el mundo real cambián todo el tiempo.
- Caminar
- El rebote de una pelota
Los suiches aparecen por diseño¶
Realizar cambio en la manera como funcionan las cosas mejora su desempeño.
- Caja de cambios
- Diferente juego de engranes
Problemas que aparecen a tener suiches¶
- ¿Cómo podemos crear estos modelos?
- ¿Son estables y tiene buen desempeño?
- ¿Podemos diseñar dichos sistemas?
- ¿Hay trampas?
Automatas híbridos¶
Necesitamos describir sistemas que contienen ambos mundos, la dinámica del sistema continuo y los cambios de la lógica discreta.
Un automata híbrido es:
Una máquina de estados finitos (lógica discreta) que incluye dinámica continua
Modos, transiciones, guardias y resets¶
- Supongamos un estado continuo para el sistema $x$ y como estaremos cambiando entre diferentes modos de operacion agreguemos un estado discreto $q$. La dinámica entonces será:
- La transicion entre diferente modos discretos puede ser representada como una maquina de estados finitos.
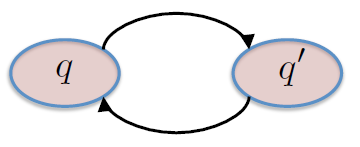
Modos, transiciones, guardias y resets¶
La condiciones en la cuales ocurre una transición la llamamos condición, ejemplo: una transición de $q$ a $q'$ ocurre si:
$$x\in G_{q,q'}$$
Como componente final, vamos a permitir cambios radicales/abruptos en los estados mientras la transición ocurre, esto son llamads reset:
$$x:=R_{q,q'}(x)$$
Modelo de los automatas híbridos¶
- Poniendo todo en conjunto obtenemos una respresentación muy rica del modelo, que se conoce como un automatata híbrido.
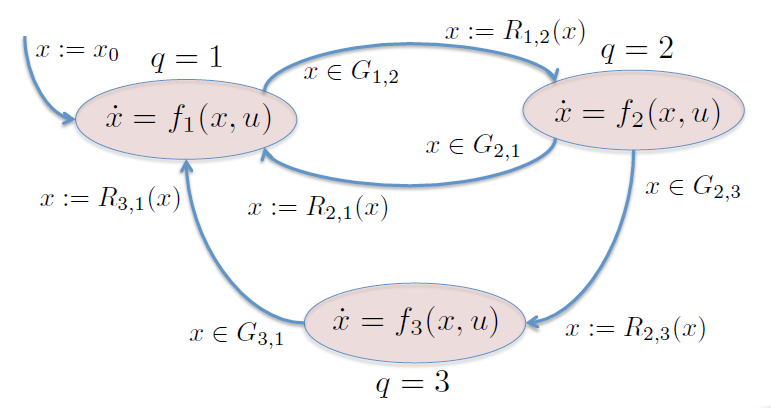
Ejemplo del modelo de temperatura de un salón¶
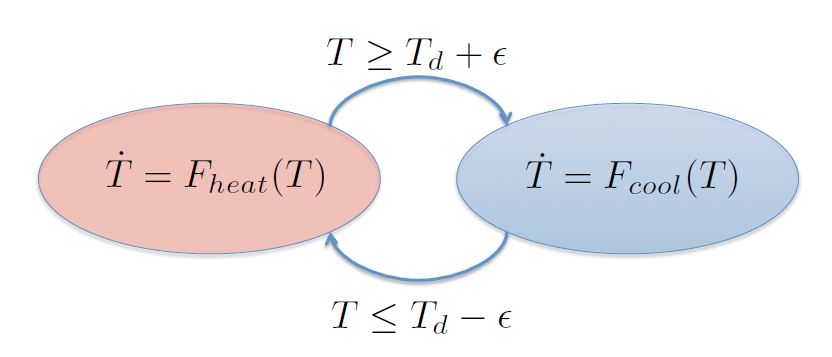
Ejemplo del modelo de una caja de cambios¶
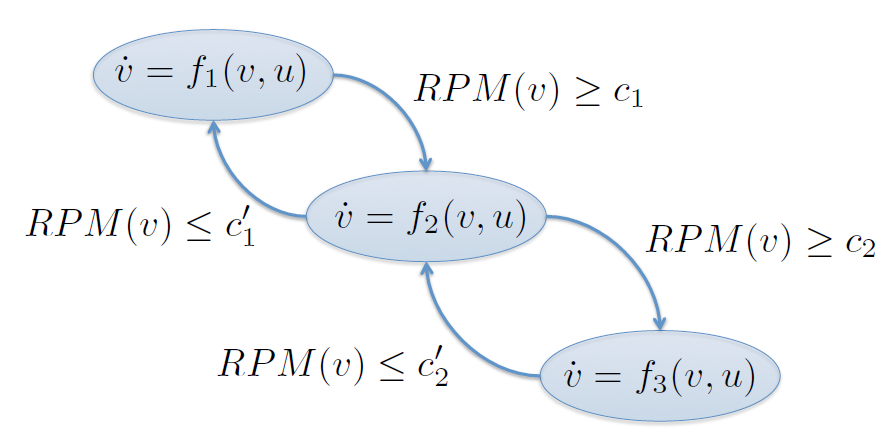
Ejemplo de un modelo basado en comportamiento¶
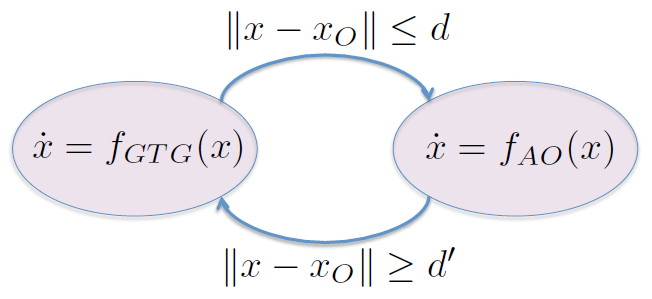
¿ Qué puede salir mal cuando empezamos a cambiar entre diferentes controladores ?¶
Un sencillo sistema con dos modos¶
$$\dot{x}=A_1\,x=\left[\array{-\epsilon&1\\-2&-\epsilon}\right]x$$$$\dot{x}=A_2\,x=\left[\array{-\epsilon&2\\-1&-\epsilon}\right]x$$$$\text{eig}(A_i)=-\epsilon\pm1.41j$$- Ambos modos son asintóticamente estables.
Modo 1¶
display(ani)
Modo 2¶
display(ani)
Automata Híbrido 1¶

display(ani)
Automata Híbrido 2¶

display(ani)
Resumen¶
display(ani)
Anotar¶
- Combinando modos estables, el resultado del sistema híbrido puede ser inestable.
- Combinando modos inestables, el resultado del sistema híbrido puede ser estable.
- Diseña modos estables pero ten cuidado del riesgo de transforma el sistema híbrido en un sistema inestable.
Hay Peligros¶
Subsistemas estables no garantizan que el sistema híbrido sea estable.
Sistemas suicheado¶
Vimos que podemos destabilizar subsistemas estables a traves de una desafortunada serie de suiches
Si ignoramos los resets podemos escribir los sistemas híbridos como sistemas suicheados:
$$\dot{x}=f_\sigma(x,u)$$donde $\sigma$ es la señal de suicheado
La señal de suicheado dicta in que modo discreto nos encontramos.
$$\sigma(t) \in \Sigma = \{1,\ldots \,,p\}$$Diferentes tipos de estabilidad¶
Dado un sistema suicheado $\dot{x}=f_\sigma(x,u)$ tendremos estabilidad:
- universal, asintoticamente estable: $$x \to 0, \forall\sigma$$
- existencial, asintoticamente estable: $$\exists \sigma \quad\text{s.t.}\quad x\to 0$$
Si la señal de suicheado es generada por un automata híbrido:
- híbrida, asintoticamente estable: $$x\to 0$$
Algunas consideraciones¶
Si todos los modos son AS entonces:
- Tendremos un sistema existencialmente AS, ya que podemos escoger un modo y no cambiamos!
- No siempre sera universalmente AS, vimos un contraejemplo.
Recomendaciones¶
- Diseñar controladores estables para los subsistemas.
- Diseña la logica suicheada en el automata híbrido.
- Esta pendiente de las posibilidades de inestabilidad y probar, probar y probar.
El modelo de la pelota que rebota en una superficie¶
La ecuación del movimiento entre rebotes es:
$$\ddot{h}=-g$$$$\dot{x}=\left[\array{0&1\\0&0}\right]x + \left[\array{0\\-g}\right] \qquad y = \left[\array{1&0}\right] x$$Los rebotes pueden ser modelados como resets:
$$\dot{h}:= - \gamma \dot{h}$$$$x:=\left[\array{1&0\\0&-\gamma}\right]x$$El automata híbrido de la pelota¶
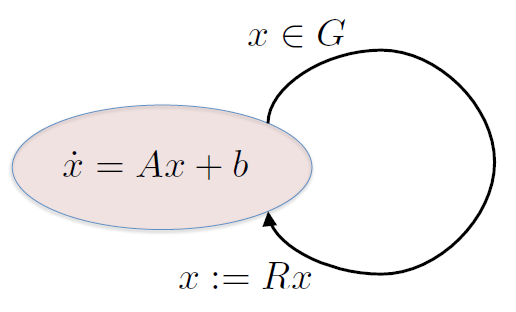
Cuál sería la condición o guardia ?
- $h\leq0 \to \left[\array{1&0}\right] x \leq0$
- $h\leq0 \:\text{y}\: \dot{h}\leq0 \to x \leq 0$
Resolviendo el sistema¶
Partiendo del sistema
$$\dot{x}=\left[\array{0&1\\0&0}\right]x + \left[\array{0\\-g}\right] \qquad y = \left[\array{1&0}\right] x$$y recordando la solución general para la ecuación en espacio de estados:
$$y=C\Phi(t,t_0)x(t_0) + C\int_{t_0}^t \Phi(t,\tau)Bu(\tau) d\tau \qquad \Phi(t,\tau)=e^{A(t-\tau)}$$Analizando la matriz dinámica de este sistema tenemos:
$$A^2 = A^3 = \ldots = 0$$luego:
$$e^{At} = \sum_{k=0}^\infty \frac{At^k}{k!} = I + At + 0 = \left[\array{1&t\\0&1}\right]$$Resolviendo el sistema¶
$$y=C\Phi(t,t_0)x(t_0) + C\int_{t_0}^t \Phi(t,\tau)Bu(\tau) d\tau \qquad \Phi(t,\tau)=e^{A(t-\tau)}$$remplazamos:
$$y=\left[\array{1&0}\right]\left[\array{1&t-t_0\\0&1}\right]\left[\array{h_0\\ \dot{h}_0}\right] + \left[\array{1&0}\right]\int_{t_0}^t \left[\array{1&t-\tau\\0&1}\right]\left[\array{0\\-g}\right] d\tau$$integrando:
$$y = h_0 + \dot{h}_0(t-t_0) - \frac{g}{2}(t-t_0)^2$$Tiempo entre rebotes¶
Partiendo de la solución y teniendo las condiciones $h_0=0$ y $t_0=0$
$$y = h_0 + \dot{h}_0(t-t_0) - \frac{g}{2}(t-t_0)^2$$El tiempo para un primer rebote será:
$$y(T)=0 = \dot{h}_0T - \frac{g}{2}T^2 = T \left(\dot{h}_0 - \frac{g}{2}T\right)$$solución:
$$T=0 \qquad T = \frac{2\dot{h}}{g}$$El tiempo entre rebotes será : $T = \frac{2\dot{h}}{g}$
Tiempo acumulado¶
Siendo $\gamma$ la fracción de energía recuperada por el sistema en el rebote tendremos y $v=\dot{h}_0$ la velocidad inicial, para los tiempos de los rebotes.
$$\array{T_1 =& 2v/g \\ T_2=& 2v/g&+\gamma 2v/g}$$Luego para el rebote $N$ tendremos :
$$T_N = \frac{2v}{g}\sum_{k=0}^{N-1}\gamma^k = \frac{2v}{g}\frac{1}{1-\gamma} \qquad \gamma<1$$Rebotes infinito en tiempo finito¶
$$T_\infty = \frac{2v}{g}\frac{1}{1-\gamma} < \infty$$La pelota rebota infinitas veces en tiempo finito. Esto es más que una curiosidad matemática.
- La simulaciones explotan.
- Los sistemas híbrido quedan indefinido despues de ese momento.
Este hecho se conoce como el fenómemo de Zenón.
El fenómeno/paradoja de Zenón¶
Zenón de Elea (490ac-430ac)
"In a race, the quickest runner can never over take the slowest, since the pursuer must first reach the point whence the pursued started, so that the slower must always hold a lead." — as recounted by Aristotle, Physics VI:9, 239b15
- La paradoja : Aquiles nunca alcanza a la tortuga.
- La solución : La convergencia de la situación.
- El problema : Se generan infinitos suiches en tiempo finito.
Ejemplo¶
$$\dot{x}=\cases{-1& x > 0\\+1& x < 0}$$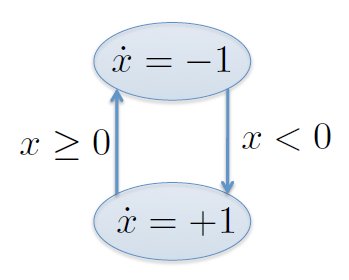
- Este sistema suichea infinitamente muchas veces en un solo instante de tiempo
- Zeno: Infinitos cambios en tiempo finito.
- Tipo 1: En un solo instante
- Tipo 2: No tipo 1 (rebote de una pelota)
Buenas y malas noticias¶
- Zeno es un problema
- Zeno Tipo 1 no es solo detectable, sino que que podemos lidiar con él de manera directa.
- Zeno Tipo 2 es en general difícil de manejar.
Superficie de deslizamiento¶
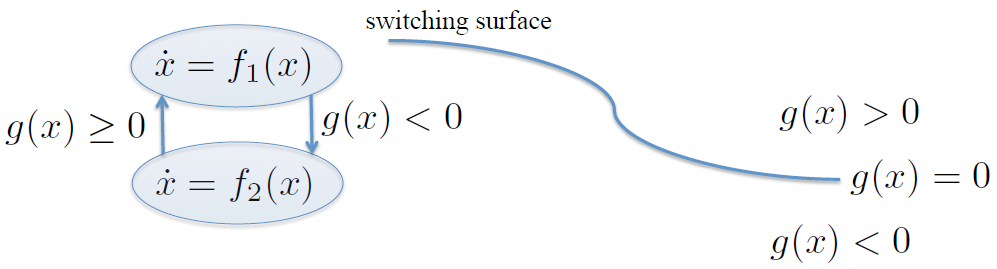
Deslizamiento¶
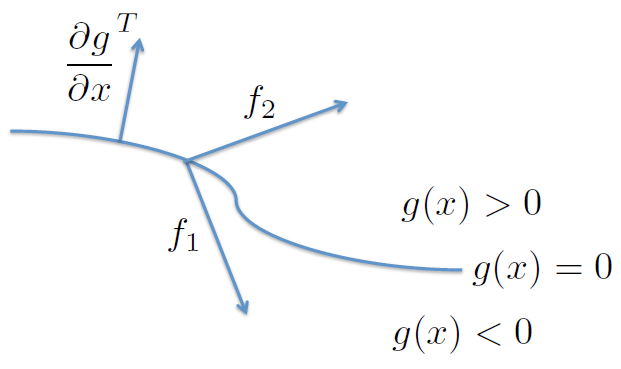
El deslizamiento ocurre cuando:
$$\frac{\partial g}{\partial x}f_1 < 0 \qquad\text{y}\qquad \frac{\partial g}{\partial x}f_2 > 0 $$La derivada de $g$ in la dirección $f$ se conoce como la derivada de Lie $L_fg$
Probando el Zeno tipo 1¶
Podemos saber si tenemos zeno tipo 1 si ocurre el deslizamiento:
$$\frac{\partial g}{\partial x}f_1 < 0 \qquad\text{y}\qquad \frac{\partial g}{\partial x}f_2 > 0 $$o escrito de otra forma
$$L_{f_1} g < 0 \qquad\text{y}\qquad L_{f_2} g > 0 $$Regularización¶
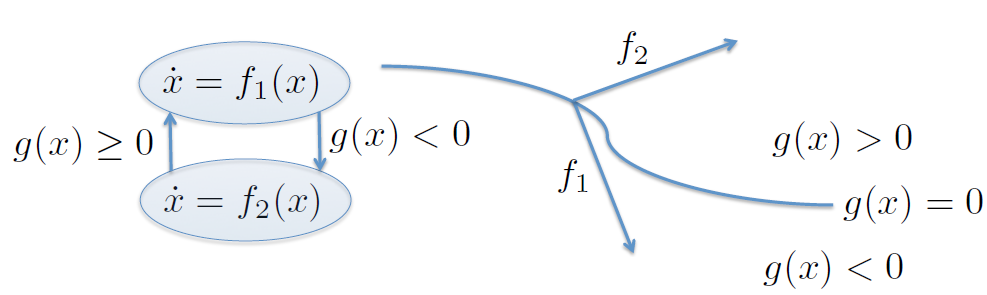
Modo Deslizante¶
El modo deslizante se da cuando $dg/dt = 0$, luego
$$\frac{dg}{dt} = \frac{\partial g}{\partial x} \dot{x} = \frac{\partial g}{\partial x}\left(\sigma_1f_1+\sigma_2f_2\right) = \sigma_1L_{f_1}g+\sigma_2L_{f_2}g$$de aquí:
$$\sigma_2 = -\sigma_1 \frac{L_{f_1}g}{L_{f_2}g}$$con lo anterior podemos calcular los valores $\sigma_1$ y $\sigma_2$ del modo deslizante. Teniendo en cuenta que:
$$\array{\sigma_1,\sigma_2 \geq 0 &\text{y}& \sigma_1+\sigma_2 = 1}$$Modo inducido¶
De las ecuaciones anteriores podemos definir:
$$\sigma_2 = -\sigma_1 \frac{L_{f_1}g}{L_{f_2}g}$$$$\sigma_1+\sigma_2 = \sigma_1 \left(1-\frac{L_{f_1}g}{L_{f_2}g}\right)= 1$$de aquí:
$$\array{\sigma_1 = \frac{L_{f_2}g}{L_{f_2}g-L_{f_1}g}&&\sigma_2 = -\frac{L_{f_1}g}{L_{f_2}g-L_{f_1}g}}$$el modo inducido será:
$$\dot{x} = \frac{1}{L_{f_2}g-L_{f_1}g}\left(L_{f_2}g\,f_1-L_{f_1}g\,f_2\right)$$Regularización de Zeno tipo 1¶