Sistemas Lineales¶
Adentrandonos en la matemática del asunto
Controlando una masa puntual¶
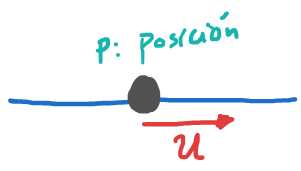
Dada una masa puntual sobre una linea, cuya aceleración is directamente controlada:
$$\ddot{p} = u$$Escribiendo la ecuación diferencial en una forma más general (espacio de estados tenemos):
$$\array{ x_1 = p &&& \dot{x}_1 = x_2 \\ x_2 = \dot{p} &&& \dot{x}_2 = u }$$Forma de la ecuación en espacio de estados¶
Tenemos que la derivada de la posición ($x_1$) es la velocidad $\dot{x}_1 = x_2$ y que la derivada de la velocidad ($x_2$) es la aceleración $\dot{x}_2=u$, el estado del sistema es "2-dimensional":
$$x=\left[\array{x_1\\x_2}\right]$$La ecuación de estado es:
$$\dot{x}=\left[\array{\dot{x}_1\\\dot{x}_2}\right]=\left[\array{x_2\\u}\right]=\left[\array{0&1\\0&0}\right]\left[\array{x_1\\x_2}\right]+\left[\array{0\\1}\right]u$$La ecuación de salida es:
$$y=p=x_1=\left[\array{1&0}\right]x$$Forma general del espacio de estados¶
Teniendo esto,
$$\dot{x}=\left[\array{\dot{x}_1\\\dot{x}_2}\right]=\left[\array{x_2\\u}\right]=\left[\array{0&1\\0&0}\right]\left[\array{x_1\\x_2}\right]+\left[\array{0\\1}\right]u$$$$y=p=x_1=\left[\array{1&0}\right]x$$Podemos llevarlo a:
$$\array{\dot{x}=Ax+Bu\\y=Cx}$$donde, para este caso:
$$\array{A=\left[\array{0&1\\0&0}\right]&B=\left[\array{0\\1}\right]&C=\left[\array{1&0}\right]}$$Caso para un masa puntual en dos dimensiones¶
Teniendo las ecuaciones diferenciales :
$$\array{\ddot{p}_x=u_x&&&\ddot{p}_y=u_y}$$encontrar las matrices $A$, $B$ y $C$.
siendo:
- el estado del sistema $$x^T=\left[\array{p_x&\dot{p}_x&p_y&\dot{p}_y}\right]^T$$
- la entrada del sistema $$u^T=\left[\array{u_x&u_y}\right]^T$$
- la salida del sistema $$y^T=\left[\array{p_x&p_y}\right]^T$$
Caso para un masa puntual en dos dimensiones¶
Podemos llevarlo a:
$$\array{\dot{x}=Ax+Bu\\y=Cx}$$donde, para este caso:
$$\array{A=\left[\array{0&1&0&0\\0&0&0&0\\0&0&0&1\\0&0&0&0}\right]&B=\left[\array{0&0\\1&0\\0&0\\0&1}\right]&C=\left[\array{1&0&0&0\\0&0&1&0}\right]}$$Sistema LTI¶
Los sistemas LTI (Linear Time-Invariant) se pueden representar en el espacio de estados.
$$\array{\dot{x}=Ax+Bu\\y=Cx}$$dependiento de la dimensionalidad del estado $x$, la entrada $u$ y la salida $y$. Las matrices de la ecuación anterior se veran afectadas.
$$\cases{x\in\mathfrak{R}^n\\u\in\mathfrak{R}^m\\y\in\mathfrak{R}^p} \qquad\to\qquad \array{A:n\times n\\B:n\times m\\C:p\times n}$$siendo $n$ el número de variables de estado, $m$ el número de entradas y $p$ el número de salidas
Modelo en espacio de estados¶
Teniendo el estado $x$, la entrada $u$ y la salida $y$.
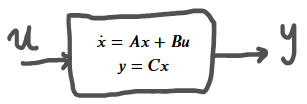
Surgen tres preguntas:
- ¿De dónde surgen dichos sistemas?
- ¿Cómo interpretar dichos sistemas?
- ¿Cómo selecionamos la entrada?
Ejemplo 1: Model del carro¶
Empezando de la ecuación diferencial :
$$\dot{v}=\frac{c}{m}\, u - \gamma\, v$$- realicemos la ecuación en espacio de estados para el control de velocidad $v$
- realicemos la ecuación en espacio de estados para el control de posición $p$
Para el control de la velocidad del carro¶
- El estado es la velocidad $x=v$, luego:
donde,
$$\array{A=\left[\array{-\gamma}\right]&B=\left[\array{\frac{c}{m}}\right]&C=\left[\array{1}\right]}$$Para el control de la posición del carro¶
- El estado es la posición y la velocidad $x^T=\left[\array{p&v}\right]$, luego:
donde,
$$\array{A=\left[\array{0&1\\0&-\gamma}\right]&B=\left[\array{0\\\frac{c}{m}}\right]&C=\left[\array{1&0}\right]}$$Ejemplo 2: Péndulo¶
De la 2da ley de Newton tenemos:
$$\ddot{\theta}=-\frac{g}{l}\sin{\theta}+c\,u$$Encontremos la ecuación en espacio de estados ⚠️
El sistema no es lineal
Aproximemos para angulos pequeños $\theta <<1 $, $\sin\theta \approx \theta$
Para angulos pequeños el pendulo¶
El estado es la posición y la velocidad angular $x^T=\left[\array{\theta&\dot\theta}\right]$, luego:
$$\array{\dot{x}=Ax+Bu\\y=Cx}$$donde,
$$\array{A=\left[\array{0&1\\-\frac{g}{l}&0}\right]&B=\left[\array{0\\c}\right]&C=\left[\array{1&0}\right]}$$Ejemplo 3: Dos robots simples sobre una linea¶
Consideremos el control de dos robots sobre una linea a los cuales se les puede dar la orden directamente en velocidad.

Encontremos la ecuación en espacio de estados ⚠️
donde,
$$\array{A=0&B=\left[\array{1&0\\0&1}\right]&C=\left[\array{1&0\\0&1}\right]}$$¿Cómo hacemos para que se encuentren en el mismo lugar?
Problema del "Rendezvous"¶
¿Cómo hacemos para que se encuentren en el mismo lugar?
Idea 💡 : Hacer que se diriga el uno al otro;
$$\cases{u_1=x_2-x_1\\u_2=x_1-x_2}$$¿Cómo queda la ecuación de estado remplazando esta ley de control?
Simulación del problema¶
display(ani)
Ejemplo 4: Robot uniciclo¶
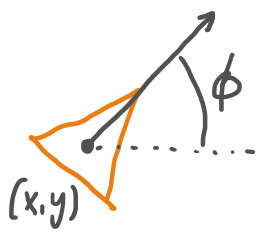
Donde sus ecuaciones diferenciales son:
$$\array{\dot{x}=v\cos\phi\\\dot{y}=v\sin\phi\\\dot\phi=w}$$el sistema es no lineal, ¿Podemos usar la aproximación de angulos pequeños?
No, sigue siendo no lineal:
$$\array{\dot{x}=v\\\dot{y}=v\phi\\\dot\phi=w}$$“Classifying systems as linear and non-linear is like
classifying objects in the Universe as bananas and
non-bananas.” - Unknown
Linealización¶
Dado un sistema no lineal:
$$\array{\dot{x}=f(x,u)&&y=h(x)}$$vamos a querer encontrar un modelo lineal "local" al rededor de un punto de operación.
$$(x_o,u_o) \to (x = x_o + \delta x, u= u_o+ \delta u)$$con esto las ecuaciones de movimiento se transforman en:
$$\dot{\delta x}=\dot{x}-\dot{x}_o = f\left(x_o + \delta x, u_o+ \delta u\right)$$Linealización¶
$$\dot{\delta x}=\dot{x}-\dot{x}_o = f\left(x_o + \delta x, u_o+ \delta u\right)$$realizando una expansión en serie de Taylor:
$$\dot{\delta x}\approx f\left(x_o,u_o\right)+\frac{\partial f}{\partial x}\left(x_o,u_o\right)\delta x + \frac{\partial f}{\partial u}\left(x_o,u_o\right)\delta u \,+ \mathscr{O}^2$$$$y=h\left(x_o+\delta x\right)\approx h\left(x_o\right)+\frac{\partial h}{\partial x}\left(x_o\right) \delta x \,+ \mathscr{O}^2$$asumiendo que:
$$\array{f\left(x_o,u_o\right)=0&&h\left(x_o\right)=0}$$Linealización¶
tendremos:
$$\array{ \cases{ \dot{x}=f(x,u)\\ y=h(x)\\ \\ f\left(x_o,u_o\right)=0\\ h\left(x_o\right)=0} && \array{x = x_o + \delta x\\u= u_o+ \delta u\\ \to} && \cases{ \dot{\delta x}=A\delta x + B\delta u \\ y = C \delta x \\ \\ A = \frac{\partial f}{\partial x}\left(x_o,u_o\right) \\ B = \frac{\partial f}{\partial u}\left(x_o,u_o\right) \\ C = \frac{\partial h}{\partial x}\left(x_o\right) } }$$Computando los Jacobianos¶
Teniendo que $x\in\mathfrak{R}^n$, $u\in\mathfrak{R}^m$, $y\in\mathfrak{R}^p$ y
$$\array{f^T = \left[\array{f_1&f_2&\cdots&f_n}\right]^T&&&h^T = \left[\array{h_1&h_2&\cdots&h_p}\right]^T}$$tendremos entonces:
$$\array{ \frac{\partial f}{\partial x} = \left[\array{ \frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_n}{\partial x_1} & \cdots & \frac{\partial f_n}{\partial x_n} \\ }\right]_{(n\times n)} && \frac{\partial f}{\partial u} = \left[\array{ \frac{\partial f_1}{\partial u_1} & \cdots & \frac{\partial f_1}{\partial u_m} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_n}{\partial u_1} & \cdots & \frac{\partial f_n}{\partial u_m} \\ }\right]_{(n\times m)} && \frac{\partial h}{\partial x} = \left[\array{ \frac{\partial h_1}{\partial x_1} & \cdots & \frac{\partial h_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial h_p}{\partial x_1} & \cdots & \frac{\partial h_p}{\partial x_n} \\ }\right]_{(p\times n)} }$$Ejemplo 5: Péndulo Invertido¶
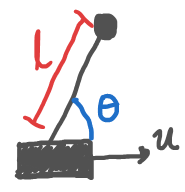
Partiendo de la ecuación diferencial:
$$\ddot{\theta} = \frac{g}{l}\sin\theta + u\cos\theta$$teniendo el estado como $x^T = \left[\array{\theta &\dot{\theta}}\right]^T$
- Definamos la ecuación de estado y de salida del sistema no linear.
- Encontremos las matrices de las ecuaciones de estados lineales, teniendo en cuenta $(x_o,u_o)=(0,0)$.
Ejemplo 6: Linealización del uniciclo¶
 $$\array{
\array{\dot{x}=v\cos\phi\\\dot{y}=v\sin\phi\\\dot\phi=w} &
\left\{\array{
x_1 = x & x_2 = y & x_3 = \phi \\
y_1 = x_1 & y_2 = x_2 & y_3 = x_3 \\
u_1 = u & u_2 = w
}\right. & (x_o,u_o)=(0,0)
}$$
$$\array{
\array{\dot{x}=v\cos\phi\\\dot{y}=v\sin\phi\\\dot\phi=w} &
\left\{\array{
x_1 = x & x_2 = y & x_3 = \phi \\
y_1 = x_1 & y_2 = x_2 & y_3 = x_3 \\
u_1 = u & u_2 = w
}\right. & (x_o,u_o)=(0,0)
}$$¿Qué pasa con $\dot{x}_2 = 0$?
Comentarios sobre la linealización¶
- Algunas veces la linealización da modelos razonables y otras veces no.
- A pesar de que son aproximaciones locales, estos modelos son muy utiles cuando funcionan.